题目内容
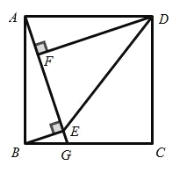
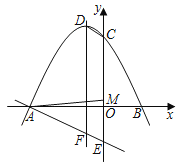
【题目】如图,已知等边△ABC,AB=12.以AB为直径的半圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连结GD.
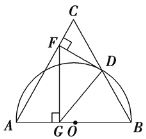
(1)求证:DF是⊙O的切线;
(2)求FG的长;
(3)求△FDG的面积.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1) 如图所示,连接OD.由题意可知∠A=∠B=∠C=60°,则OD=OB,可以证明△OBD为等边三角形,易得∠C=∠ODB=60°,再运用平行线的性质和判定以及等量代换即可完成解答.
(2)先说明OD为△ABC的中位线,得到BD=CD=6.在Rt△CDF中,由∠C=60°,得∠CDF=30°,根据含30度的直角三角形三边的关系得CF=![]() CD,则AF=AC-CF=9,最后在Rt△AFG中,根据正弦的定义即可解答;
CD,则AF=AC-CF=9,最后在Rt△AFG中,根据正弦的定义即可解答;
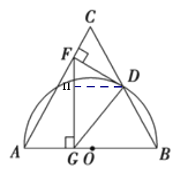
(3)作DH⊥FG,CD=6,CF=3,DF=3![]() ,FH=
,FH=![]() ,DH=
,DH=![]() ,最后根据三角形的面积公式解答即可.
,最后根据三角形的面积公式解答即可.
解:(1)如图所示,连接OD.
∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°
∵OD=OB
∴△OBD为等边三角形,
∴∠C=∠ODB=60°,
∴AC∥OD,
∴∠CFD=∠FDO,
∵DF⊥AC,
∴∠CFD=∠FDO=90°,
∴DF是⊙O的切线
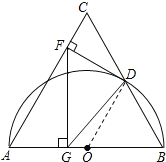
(2)因为点O是AB的中点,则OD是△ABC的中位线.
∵△ABC是等边三角形,AB=12,
∴AB= AC= BC= 12, CD=BD=![]() BC=6
BC=6
∵∠C=60°,∠CFD=90°,
∴∠CDF=30°,同理可得∠AFG=30°,
∴CF=![]() CD=3
CD=3
∴AF=12-3=9.
∴![]() .
.
(3)作DH⊥FG,CD=6,CF=3,DF=3![]()
∴FH=![]() ,DH=
,DH=![]()
∴△FDG的面积为![]() DH
DH![]() FG=
FG=![]()

【题目】学习一定要讲究方法,比如有效的预习可大幅提高听课效率.九年级(1)班学习兴趣小组为了了解全校九年级学生的预习情况,对该校九年级学生每天的课前预习时间(单位:![]() )进行了抽样调查.并将抽查得到的数据分成5组,下面是未完成的频数、顿率分布表和频数分布扇形图.
)进行了抽样调查.并将抽查得到的数据分成5组,下面是未完成的频数、顿率分布表和频数分布扇形图.
组别 | 课前预习时间 | 频数(人数) | 频率 |
1 |
| 2 | |
2 |
|
| 0.10 |
3 |
| 16 | 0.32 |
4 |
|
|
|
5 |
| 3 |
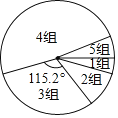
请根据图表中的信息,回答下列问题:
(1)本次调查的样本容量为 ,表中的![]() ,
,![]() ,
,![]() ;
;
(2)试计算第4组人数所对应的扇形圆心角的度数;
(3)该校九年级其有1000名学生,请估计这些学生中每天课前预习时间不少于![]() 的学生人数.
的学生人数.