题目内容
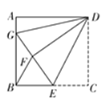
【题目】如图,在正方形ABCD中,点E是BC边的中点,将△DCE沿DE折叠,使点C落在点F处,延长EF交AB于点G,连接DG、BF.
(1)求证:DG平分∠ADF;
(2)若AB=12,求△EDG的面积.
【答案】(1)见解析;(2)60
【解析】
(1)由折叠可知,DF=DC=DA,∠DFE=∠C=90°,证明Rt△ADG≌Rt△FDG即可证明DG平分∠ADF;
(2)设AG=x,则BG=12-x,GE=x+6,在Rt△BEG中,根据勾股定理建立方程求出x,然后再求出面积即可.
解:(1)如图,由折叠可知,DF=DC=DA,∠DFE=∠C=90°,
∴∠DFG=∠A=90°,
在Rt△ADG和Rt△FDG中,
![]()
∴Rt△ADG≌Rt△FDG(HL),
∴∠ADG=∠FDG,
∴DG平分∠ADF;
(2)∵AB=12,点E是BC边的中点,
∴BE=CE=6,
∴EF=6,
设AG=x,
∴GF=x,BG=12-x,
∴GE=x+6,
在Rt△BEG中,
![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴GE=4+6=10,
∴S△EDG=10×12×![]() =60.
=60.

练习册系列答案
相关题目