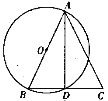
[题目]如图.在平面直角坐标系中.点为坐标原点.将含30°角的放在第一象限.其中30°角的对边长为1.斜边的端点.分别在轴的正半轴.轴的正半轴上滑动.连接.则线段的长的最大值是( )A.2B.C.D. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，在平面直角坐标系中，点为坐标原点，将含30°角的放在第一象限，其中30°角的对边长为1，斜边的端点，分别在轴的正半轴，轴的正半轴上滑动，连接，则线段的长的最大值是（）

A.2B.C.D.

【答案】A

【解析】

取AB的中点F，连接CF、OF．首先求出OF=FC=1，根据三角形的三边关系可知：OC≤OF+OC，推出当O、F、C共线时，OC的值最大，最大值为2．

解：取AB的中点F，连接CF、OF．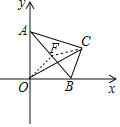

在Rt△ABC中，∵∠ACB=90°，∠BAC=30°，BC=1，
∴AB=2BC=2，
∵∠AOB=90°，AF=FB，
∴OF=FC=AB=1，
∵OC≤OF+CF，
∴当O、F、C共线时，OC的值最大，最大值为2．
故选：A．

练习册系列答案

你添加的条件是

【题目】如图，二次函数y＝ax2+2ax+c（a＜0）的图象与x轴交于A、B两点，与y轴交于C点，顶点为D，一次函数y＝mx﹣3的图象与y轴交于E点，与二次函数的对称轴交于F点，且tan∠FDC＝．

（1）求a的值；

（2）若四边形DCEF为平行四边形，求二次函数表达式．

（3）在（2）的条件下设点M是线段OC上一点，连接AM，点P从点A出发，先以1个单位长度/s的速度沿线段AM到达点M，再以个单位长度/s的速度沿MC到达点C，求点P到达点C所用最短时间为　 s（直接写出答案）．

【题目】在同一直角坐标系中，函数y＝kx+1与y＝﹣（k≠0）的图象大致是（　　）

A.B.

C.D.

【题目】如图，在平面直角坐标系中，点O为坐标原点，直线y＝﹣x+b交y轴于点A，交x轴于点B，S△AOB＝．

（1）求b的值；

（2）点C以每秒1个单位长度的速度从O点出发沿x轴向点B运动，点D以每秒2个单位长度的速度从A点出发沿y轴向点O运动，C，D两点同时出发，当点D运动到点O时，C，D两点同时停止运动．连接CD，设点C的运动时间为t秒，△CDO的面积为S，求S与t的函数关系式（不要求写出自变量t的取值范围）；

（3）在（2）条件下，过点C作CE⊥CD交AB于点E，过点D作DF∥x轴交AB于点F，过点F作FH⊥CE，垂足为H．在CH上取点M，使得MH：HE＝8：33，连接FM，若∠FMH＝∠FEH，求t的值．

【题目】人在运动时的心跳速率通常和人的年龄有关．如果用表示一个人的年龄，用表示正常情况下这个人在运动时所能承受的每分心跳的最高次数，那么．

（1）一个45岁的人运动时10秒心跳的次数为22次，他__________（填“有”或“无”）危险；

（2）即将参加中考的两名同学的对话：甲同学：“我正常情况下在运动时所能承受的每分心跳的最高次数是164次”，乙同学：“我正常情况下在运动时所能承受的每分心跳的最高次数才156次”．请你判断甲乙两名同学谁的说法是错误的？并说明理由．

（3）若一个人的年龄由变为（为正整数），发现正常情况下这个人在运动时所能承受的每分心跳的最高次数减少了12，用列方程的方法确定．

【题目】如图，在等腰中，点为直线上一动点(点不与、重合)．以为边向右侧作正方形，连结．

（猜想）如图①，当点在线段上时，直接写出、、三条线段的数量关系．

（探究）如图②，当点在线段的延长线上时，判断、、三条线段的数量关系，并说明理由．

（应用）如图③，当点在线段的反向延长线上时，点、分别在直线两侧，、交点为点连结，若，，则　　　　．

【题目】学习一定要讲究方法，比如有效的预习可大幅提高听课效率．九年级（1）班学习兴趣小组为了了解全校九年级学生的预习情况，对该校九年级学生每天的课前预习时间（单位：）进行了抽样调查．并将抽查得到的数据分成5组，下面是未完成的频数、顿率分布表和频数分布扇形图．

组别	课前预习时间	频数（人数）	频率
1		2
2			0.10
3		16	0.32
4
5		3

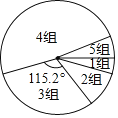
请根据图表中的信息，回答下列问题：

（1）本次调查的样本容量为，表中的，，；

（2）试计算第4组人数所对应的扇形圆心角的度数；

（3）该校九年级其有1000名学生，请估计这些学生中每天课前预习时间不少于的学生人数．

【题目】如图，点在直线上，过点作，且，点在射线上（点不与点重合），且满足，，与交于点，过点作于点．设．

（1）用含的代数式表示的长；

（2）①线段的长是________；

②线段的长是_________；（用含的代数式表示）

（3）当为何值时，有最小值？并求出这个最小值．

试题分类