题目内容
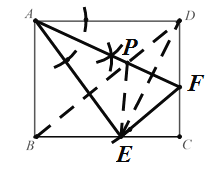
【题目】四边形ABCD是一个长方形，将AD沿某一直线AF（F为折痕与CD边的交点）折叠，使点D落在BC边上的某一点E处，请用没有刻度的直尺与圆规找出点E与折痕AF，并在折痕AF上找一点P满足BP＋EP最小．
【答案】见详解.
【解析】
根据题意，以A为圆心，AD长为半径画弧，与边BC相交于点E，连接AE，作∠DAE的角平分线，交CD于点F ，连接AF即可；连接DE ，由点E与点D关于AF对称，则连接BD，与AF相交于点P，连接PE ，此时BP＋EP为最小值.
解：如图：
①以A为圆心，AD长为半径画弧，与边BC相交于点E，连接AE，即点E为所求点；
②作∠DAE的角平分线，交CD于点F ，连接AF，即AF为折痕；
③连接DE，由DF=EF，则AF垂直平分DE，
∴点D与点E关于AF对称，则
连接BD，BD与AF相交于点P，连接PE，则PE=PD，此时PE+PB为最小值.
最小值为：PE+PB=PD+PB=BD.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】为保护和改善环境，发展新经济，国家出台了不限行、不限购等诸多新能源汽车优惠政策鼓励新能源汽车的发展，为响应号召，某市某汽车专卖店销售A，B两种型号的新能源汽车共25辆，这两种型号的新能源汽车的进价、售价如下表：
进价 | 售价 | |
A型 | 10 |
|
B型 | 15 |
|
如何进货，进货款恰好为325万元？
如何进货，该专卖店售完A，B两种型号的新能源汽车后获利最多且不超过进货价的
，此时利润为多少元？
