题目内容
【题目】如图，一段抛物线：
，记为
，它与x轴交于点O，
；将绕点旋转
得
，交x轴于点
；将绕点旋转得
，交x轴于点
；
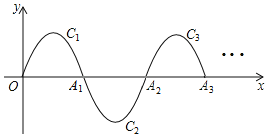
如此进行下去，得到一“波浪线”，若点
在此“波浪线”上，则m的值为
A. 4 B. 
C. 
D. 6
【答案】C
【解析】
先解方程得到-x（x-5）=0得A1（5，0），则OA1=5，利用旋转性质得A1A2=A2A3=…=OA1=5，再利用抛物线的性质可确定抛物线C404的解析式为y=（x-2015）（x-2020），然后计算自变量为2018时的函数值即可得到m的值．
当y=0时，-x（x-5）=0，解得x1=0，x2=5，则A1（5，0），
∴OA1=5，
∵将C1绕点A1旋转180°得C2，交x轴于点A2；将C2绕点A2旋转180°得C3，交x轴于点A3；…如此进行下去，得到一“波浪线”，
∴A1A2=A2A3=…=OA1=5，
∴抛物线C404的解析式为y=（x-5×403）（x-6×404），即y=（x-2015）（x-2020），
当x=2018时，y=（2018-2015）（2018-2020）=-6，
即m=-6．
故选C．
练习册系列答案
相关题目
