题目内容
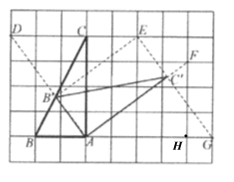
【题目】如图,在每个小正方形的边长为1的网格中,![]() 的顶点
的顶点![]() ,
,![]() ,
,![]() 均在格点上.
均在格点上.
(Ⅰ)![]() 的长等于________________;
的长等于________________;
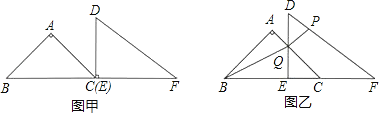
(Ⅱ)在如图所示的网格中,将![]() 绕点A旋转,使得点B的对应点
绕点A旋转,使得点B的对应点![]() 落在边
落在边![]() 上,得到
上,得到![]() ,请用无刻度的直尺,画出
,请用无刻度的直尺,画出![]() ,并简要说明这个三角形的各个顶点是如何找到的(不要求证明).
,并简要说明这个三角形的各个顶点是如何找到的(不要求证明).

【答案】(Ⅰ)![]() ;(Ⅱ)图见解析,说明见解析.
;(Ⅱ)图见解析,说明见解析.
【解析】
(Ⅰ)结合网格特点和勾股定理即可得;
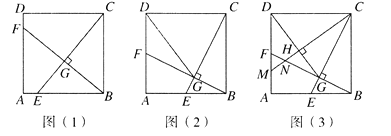
(Ⅱ)如图(见解析),取格点![]() ,
,![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,交边
,交边![]() 于点
于点![]() ,连接
,连接![]() 和
和![]() ,相交于点
,相交于点![]() ,则
,则![]() 即为所求.
即为所求.
(Ⅰ)由图可知,![]()
则![]()
故答案为:![]() ;
;
(Ⅱ)如图,取格点![]() ,
,![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,交边
,交边![]() 于点
于点![]() ,连接
,连接![]() 和
和![]() ,相交于点
,相交于点![]() ,则
,则![]() 即为所求
即为所求
证明:![]()
![]()
![]()
![]()
![]()
解得![]()
经检验,![]() 是分式方程的解
是分式方程的解
![]() 满足旋转的性质,则点
满足旋转的性质,则点![]() 为点B旋转后的对应点
为点B旋转后的对应点
在![]() 中,
中,![]()
在![]() 中,
中,![]()
![]()
![]()
![]() ,即
,即![]()
![]() 满足旋转的性质,则点
满足旋转的性质,则点![]() 在直线AF上
在直线AF上
![]()
![]() 四边形ADEG是平行四边形
四边形ADEG是平行四边形
![]()
![]() ,即
,即![]() 是直角三角形
是直角三角形
![]()
![]()
在![]() 中,
中,![]() ,即
,即![]()
解得![]()
![]() 满足旋转的性质,则点
满足旋转的性质,则点![]() 为点C旋转后的对应点
为点C旋转后的对应点
综上,顺次连接点![]() 可得到
可得到![]() .
.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
【题目】小王计划批发“山东大樱桃”和“泰国榴莲”两个品种的水果共120斤,樱桃和榴莲的批发价分别为32元/斤和40元/斤.设购买了樱桃x斤![]() .
.
(1)若小王批发这两种水果正好花费了4400元,那么小王分别购买了多少斤樱桃和榴莲?填写下表,并列方程求解;
品种 | 批发价(元) | 购买斤数 | 小王应付的钱数(元) |
樱桃 | 32 | x | |
榴莲 | 40 |
(2)设小王购买两种水果的总花费为y元,试写出y与x之间的函数表达式.
(3)若要求所批发的榴莲的斤数不少于樱桃斤数的2倍,那么购买樱桃的数量为多少时,可使小王的总花费最少?这个最少花费是多少?