题目内容
【题目】在平面直角坐标系xOy中，函数y= 
（k1＞0，x＞0）、函数y= 
（k2＜0，x＜0）的图象分别经过OABC的顶点A、C，点B在y轴正半轴上，AD⊥x轴于点D，CE⊥x轴于点E，若|k1|：|k2|=9：4，则AD：CE的值为（ ）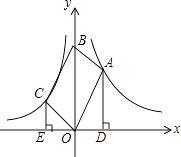
A.4：9
B.2：3
C.3：2
D.9：4
【答案】D
【解析】解：作AF⊥OB于F，如图所示：
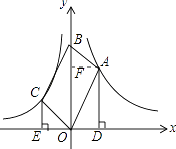
则∠AFB=∠OEC=∠ADO=90°，AF=OD，CE∥OB，
∴∠OCE=∠BOC，
∵四边形OABC是平行四边形，
∴OC=AB，OC∥AB，
∴∠ABF=∠BOC，
∴∠ABF=∠OCE，
在△ABF和△OCE中，
，
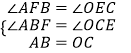∴△ABF≌△OCE（AAS），
∴AF=OE，
∴OD=OE，
∵△AOD的面积= 
ADOD= k1，△OCE的面积= CEOE= |k2|，|k1|：|k2|=9：4，
∴ 
= 
= 
．
所以答案是：D．
【考点精析】掌握平行四边形的性质是解答本题的根本，需要知道平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分．
练习册系列答案
相关题目
【题目】某食品厂从生产的袋装食品中抽出样品20袋，检测每袋的质量是否符合标准，超过或不足的部分分别用正、负数来表示，记录如下表：
与标准质量的差值 |
|
| 0 | 1 | 3 | 6 |
袋 数 | 1 | 4 | 3 | 4 | 5 | 3 |
（1）这批样品的平均质量比标准质量多还是少？多或少几克？
（2）若每袋标准质量为450克，则抽样检测的总质量是多少？
