题目内容
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC,CD⊥AB于D点,M,N是AC,BC上的动点,且∠MDN=90°,下列结论:①AM=CN;②四边形MDNC的面积为定值;③AM2+BN2=MN2;④NM平分∠CND.其中正确的是 ( )
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
【答案】A．
【解析】
试题解析：∵∠ACB=90°，AC=BC，CD⊥AB，
∴∠ADC=∠BDC=90°，AD=BD=CD=
AB，∠ACD=∠BCD=∠A=∠B=45°．
∵∠MDN=90°，
∴∠ADM=∠CDN．
在△AMD和△CND中，
，
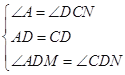∴△AMD≌△CND（ASA），
∴AM=CN，DM=DN，S△AMD=S△CND．
∴CM=BN．
∵四边形MDNC的面积=S△CDM+S△CDN=S△CDM+S△ADM=S△ADC．故为定值．
∵CM2+CN2=MN2，
∴BN2+AM2=MN2．
当MN∥AB时，MN平分∠CND．
∴正确的有：①②③．
故选A．
练习册系列答案
相关题目
【题目】小明在某商店购买商品A，B共3次，只有一次购买时，商品同时打折，其余两次均按标价购买，三次购买商品A，B的数量和费用如下表：
购买商品A的数量(个) | 购买商品B的数量(个) | 购买总费用(元) | |
第一次购买 | 7 | 6 | 1350 |
第二次购买 | 4 | 8 | 1320 |
第三次购买 | 10 | 9 | 1188 |
（1）小明以折扣价购买商品的是第_____次购物；
（2）求商品A，B的标价；
（3）若商品A，B的折扣相同，问商店是打几折出售的这两种商品．
