题目内容
【题目】画出函数y=2x+4的图像,并结合图像解决下列问题:
(1)写出方程2x+4=0的解;
(2)当﹣4≤y时,求相应x的取值范围.
【答案】(1)x=-2;(2)x≥-4.
【解析】
利用“两点确定一条直线”作出函数y=2x+4的图象.
(1)根据图象直接写出方程2x+4=0的解;
(2)根据一次函数图象的增减性写出当-4≤y时,x的取值范围.
解:∵函数的解析式为y=2x+4,
∴当x=0时,y=4.当y=0时,x=-2.即直线y=2x+4经过点(0,4),(-2,0).其图象如图所示:
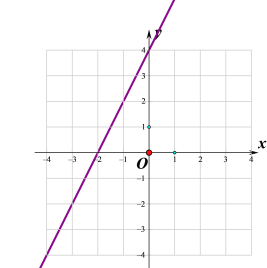
(1)根据图象知,当y=0时,x=-2,即方程2x+4=0的解是x=-2;
(2)∵y=2x+4,
∴当y=-4时,x=-4,
根据图象知,y随x的增大而增大,所以当-4≤y时,x的取值范围是x≥-4.
故答案为:(1)x=-2;(2)x≥-4.

练习册系列答案
相关题目