题目内容
【题目】如图,在△ABC中,AB=AC=4,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC分别交AB,AC于M、N,则△AMN的周长为( )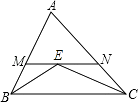
A.12
B.4
C.8
D.不确定
【答案】C
【解析】解:∵∠ABC和∠ACB的平分线交于点E,
∴∠ABE=∠CBE,∠ACE=∠BCE,
∵MN∥BC,
∴∠CBE=∠BEM,∠BCE=∠CEN,
∴∠ABE=∠BEM,∠ACE=∠CEN,
∴BM=ME,CN=NE,
∴△AMN的周长=AM+ME+AN+NE=AB+AC,
∵AB=AC=4,
∴△AMN的周长=4+4=8.
所以答案是:C.
【考点精析】通过灵活运用角的平分线和平行线的性质,掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补即可以解答此题.

练习册系列答案
相关题目