题目内容
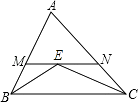
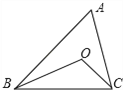
【题目】如图所示，在△ABC中，D是BC边上一点∠1＝∠2，∠3＝∠4，∠BAC＝69°，求∠DAC的度数．
【答案】32°
【解析】
设∠1=∠2=x，根据三角形外角的性质可得∠4=∠3=2x，在△ABC中，根据三角形的内角和定理可得方程2x+x+69°=180°，解方程求得x的值，即可求得∠4、∠3的度数，在△ADC中，根据三角形的内角和定理求得∠DAC的度数即可.
设∠1=∠2=x
∴∠4=∠3=∠1+∠2=2x，
在△ABC中，∠4+∠2+∠BAC=180°，
∴2x+x+69°=180°
解得x=37.
即∠1=∠2=37°，∠4=∠3=37°×2=74°.
在△ADC中，∠4+∠3+∠DAC=180°
∴∠DAC=180-∠4-∠3=180°-74°-74°=32.
练习册系列答案
相关题目
【题目】某地新建的一个企业，每月将生产1960吨污水，为保护环境，该企业计划购置污水处理器，并在如下两个型号种选择：
污水处理器型号 | A型 | B型 |
处理污水能力（吨/月） | 240 | 180 |
已知商家售出的2台A型、3台B型污水处理器的总价为44万元，售出的1台A型、4台B型污水处理器的总价为42万元．
（1）求每台A型、B型污水处理器的价格；
（2）为确保将每月产生的污水全部处理完，该企业决定购买上述的污水处理器，那么他们至少要支付多少钱？
