Question

【题目】阅读并填空完善下列证明过程：

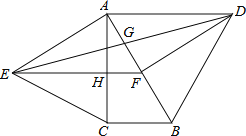
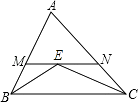
如图，已知BC⊥AC于C，DF⊥AC于D，∠1+∠2=180°，

求证：∠GFB=∠DEF﹒

证明：∵BC⊥AC于C，DF⊥AC于D（已知），

∴∠C=∠　　　　=90°（　　），

∴CB∥FD（同位角相等，两直线平行），

∴∠1+∠3=180°（　　）

又∵∠1+∠2=180°（已知），

∴∠2=∠3（　　），

∴　　　　∥　　　　（　　），

∴∠GFB=∠DEF（　　）

Answer 1

【答案】ADF；垂直的定义；两直线平行，同旁内角互补；同角的补角相等；DE；FG；内错角相等，两直线平行；两直线平行，同位角相等．

【解析】

首先根据，可以得到，这是利用垂直的定义；其次由得到，这是根据同位角相等，两直线平行；紧接着由得到，这是根据两直线平行，同旁内角互补；而已知条件中有，所以利用同角的补角相等得到，所以，这是根据内错角相等，两直线平行；由便可以得到，这是根据两直线平行，同位角相等；

∵于，于（已知），

∴ （垂直的定义），

∴（同位角相等，两直线平行 ），

∴（两直线平行，同旁内角互补）

又∵ （已知），

∴（同角的补角相等），

∴（内错角相等，两直线平行），

∴（两直线平行，同位角相等）．