题目内容
【题目】已知,正方形ABCD,G是BC边上ー点,连接AG,分别以AG和BG为直角边作等腰Rt△AGF和等腰Rt△GBE,使∠GBE=∠AGF=90°,点E,F在BC下方,连接EF.
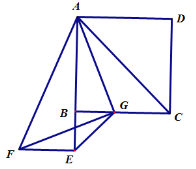
求证:①∠BAG=∠BGF,
②CG=EF:
【答案】(1)详见解析;(2)详见解析
【解析】
(1)利用正方形的性质得到∠GAB+∠AGB=90°,再利用根据同角的余角相等证明即可;
(2)连接CE,先证明△ABG≌△CBE,再利用全等三角形的性质证明四边形GFEC是平行边形形,即可解答.
证明:①∵四边形ABCD是正方形
∴∠ABC=90°,AB=CB
∴∠GAB+∠AGB=90°
∵∠AGF=90°
∴∠AGB+∠BGF=90°
∴∠BAG=∠BGF
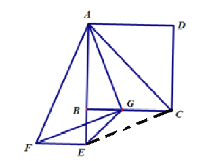
②连接CE.
∵GB=BE,∠ABG=∠GBE=90°
∴△ABG≌△CBE(SAS)
∴CE=AG ∠BCE=∠BAG
∴∠BCE=∠BGF
∴GF∥CE
∵AG=FG
∴FG=CE
∴四边形GFEC是平行边形形
∴CF=EF

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
【题目】若二次函数y=ax2+bx+c的x与y的部分对应值如下表:则下列说法错误的是( )
x | … | -1 | 0 | 1 | 2 | 3 | … |
y | … |
|
|
|
|
| … |
A. 二次函数图像与x轴交点有两个
B. x≥2时y随x的增大而增大
C. 二次函数图像与x轴交点横坐标一个在-1~0之间,另一个在2~3之间
D. 对称轴为直线x=1.5