题目内容
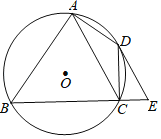
【题目】如图,在四边形![]() 中,
中,![]() 且
且![]() ,点
,点![]() 为
为![]() 中点,连接
中点,连接![]() 、
、![]() 交于点
交于点![]() .
.
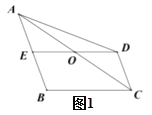
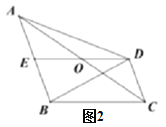
(1)如图1,求证:![]() ;
;
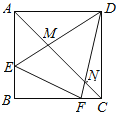
(2)如图2,连接![]() ,请直接写出图中面积等于
,请直接写出图中面积等于![]() 面积2倍的三角形.
面积2倍的三角形.
【答案】(1)见详解;(2)△AED,△BED,△BCD,△ACD.
【解析】
(1)连接CE,由![]() ,
,![]() ,
,![]() ,即可证明四边形AECD是平行四边形,即可得到OA=OC;
,即可证明四边形AECD是平行四边形,即可得到OA=OC;
(2)由(1)可知,四边形BCDE是平行四边形,则BC∥DE,BC=DE=2OE=2OD,AE=BE=CD,根据高相等,底边是OD的两倍,即可得到答案.
解:(1)如图,连接CE,
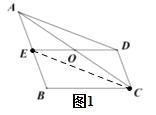
∵点![]() 为
为![]() 中点,
中点,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴四边形AECD和四边形BCDE都是平行四边形,
∴![]() ,
,![]() ;
;
(2)如图2,
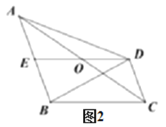
由(1)可知,四边形BCDE是平行四边形,![]()
∴BC∥DE,BC=DE=2OE=2OD,AE=BE=CD,
∴点A到DE的距离等于点D到直线BC的距离,也等于B到DE的距离,
即△AOD,△AED,△BED,△BCD,△AOE,△COD的高相等.
∴![]() ,
,
∴等于![]() 面积2倍的三角形有:△AED,△BED,△BCD,△ACD.
面积2倍的三角形有:△AED,△BED,△BCD,△ACD.

练习册系列答案
相关题目