题目内容
如图,梯形ABCD中,AD∥BC,∠C=90°,且AB=AD,连接BD,过点A作BD的垂线,交BC于E,若EC=3cm,CD=4cm,则梯形ABCD的面积是_________cm².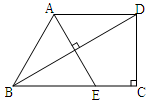

26
试题分析:连接DE,先根据勾股定理求得DE的长,由AB=AD,AE⊥BD可得AE垂直平分BD,∠BAE=∠DAE,即可得到BE的长,根据平行线的性质可得∠DAE=∠AEB,即可求得AB、BC的长,最后根据梯形的面积公式求解.
解:连接DE
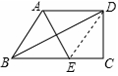
在直角三角形CDE中,根据勾股定理,得DE=5.
∵AB=AD,AE⊥BD,
∴AE垂直平分BD,∠BAE=∠DAE.
∴DE=BE=5.
∵AD∥BC,
∴∠DAE=∠AEB
∴∠BAE=∠AEB
∴AB=BE=5
∴BC=BE+EC=8
∴AD=5
∴该梯形的面积是(5+8)×4÷2=26 cm².
点评:此类问题知识点较多,综合性强,是中考常见题,一般难度较大,需特别注意.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目

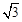 ,则AB的长是 .
,则AB的长是 .