题目内容
【题目】新规定:点![]() 为线段
为线段![]() 上一点,当
上一点,当![]() 或
或![]() 时,我们就规定
时,我们就规定![]() 为线段
为线段![]() 的“三倍距点”。如图,在数轴上,点
的“三倍距点”。如图,在数轴上,点![]() 所表示的数为-3,点
所表示的数为-3,点![]() 所表示的数为5.
所表示的数为5.

(1)确定点![]() 所表示的数为___________.
所表示的数为___________.
(2)若动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 方向以每秒2个单位长度的速度运动,设运动时间为
方向以每秒2个单位长度的速度运动,设运动时间为![]() 秒.
秒.
①当点![]() 与点
与点![]() 重合时,求
重合时,求![]() 的值.
的值.
②求![]() 的长度(用含
的长度(用含![]() 的代数式表示).
的代数式表示).
③当点![]() 为线段
为线段![]() 的“三倍距点”时,直接写出
的“三倍距点”时,直接写出![]() 的值.
的值.
【答案】(1)1或3;(2)①4;②当点P在点A右侧时,![]() ;当点P在点A左侧时,
;当点P在点A左侧时,![]() ;③16或
;③16或![]() .
.
【解析】
(1)设点C所表示的数为c,根据定义即可求出答案;
(2)①根据路程、时间、速度之间的关系即可求出答案;
②根据点P的位置即可求出AP的表达式;
③根据“三倍距点”的定义列出方程求出答案即可.
解:(1)设点C所表示的数为c,
当CA=3CB时,
c+3=3(5c),
解得:c=3,
当CB=3CA时,
5c=3(c+3),
解得:c=1
故答案为:1或3.
(2)①∵![]() ,
,
∴t=8÷2=4,
答:当点P与点A重合时,t的值为4.
②当点P在点A右侧时,![]() ;
;
当点P在点A左侧时,![]() .
.
③设点P所表示的数为p,
当PA=3AB时,
此时3p=3×8,
解得:p=27,
∴BP=5+27=32,
∴![]() ,
,
当AB=3PA时,
∴8=3(3p),
解得:![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴综上所述,t=16或![]() .
.

【题目】某校数学兴趣小组根据学习函数的经验,对函数y=![]() |x|+1的图象和性质进行了探究,探究过程如下:(1)自变量x的取值范围是全体实数,x与y的几组对应值如表:
|x|+1的图象和性质进行了探究,探究过程如下:(1)自变量x的取值范围是全体实数,x与y的几组对应值如表:
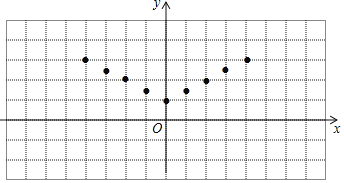
X | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
Y | … | 3 | 2.5 | m | 1.5 | 1 | 1.5 | 2 | 2.5 | 3 | … |
(1)其中m= .
(2)如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(3)当2<y≤3时,x的取值范围为 .