题目内容
【题目】某校数学兴趣小组根据学习函数的经验，对函数y＝
|x|+1的图象和性质进行了探究，探究过程如下：（1）自变量x的取值范围是全体实数，x与y的几组对应值如表：
X | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
Y | … | 3 | 2.5 | m | 1.5 | 1 | 1.5 | 2 | 2.5 | 3 | … |
（1）其中m＝ ．
（2）如图，在平面直角坐标系xOy中，描出了上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；
（3）当2＜y≤3时，x的取值范围为 ．
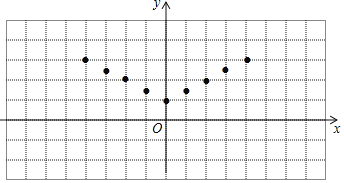
【答案】（1）2；（2）见解析；（3）﹣4≤x＜﹣2或2＜x≤4
【解析】
（1）依据在y＝
|x|+1中，令x＝﹣2，则y＝2，可得m的值；
（2）将图中的各点用平滑的曲线连接，即可画出该函数的图象；
（3）依据函数图象，即可得到当2＜y≤3时，x的取值范围．
（1）在y＝|x|+1中，令x＝﹣2，则y＝2，
∴m＝2，
故答案为：2；
（2）如图所示：
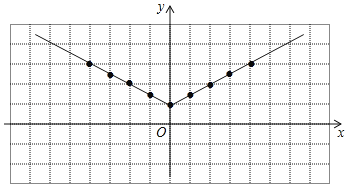
（3）由图可得，当2＜y≤3时，x的取值范围为﹣4≤x＜﹣2或2＜x≤4．
故答案为：﹣4≤x＜﹣2或2＜x≤4．
练习册系列答案
相关题目
【题目】垫球是排球运动的一项重要技术．下列图表中的数据分别是甲、乙、内三个运动员十次垫球测试的成绩，规则为每次测试连续垫球10个，每垫球到位1个记1分．
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩（分） | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
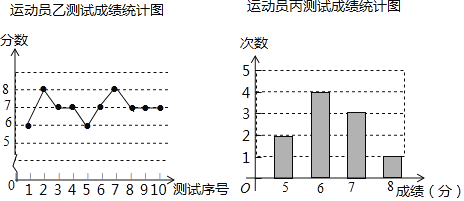
（1）写出运动员甲测试成绩的众数和中位数；
（2）试从平均数和方差两个角度综合分析，若在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人，你认为选谁更合适？（参考数据：三人成绩的方差分别为S甲2＝0.8、S乙2＝0.4、s丙2＝0.81）
