题目内容
【题目】如图,在矩形![]() 中,对角线
中,对角线![]() 的垂直平分线
的垂直平分线![]() 与
与![]() 相交于点
相交于点![]() ,与
,与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,
,![]() .求证:四边形
.求证:四边形![]() 是菱形;
是菱形;
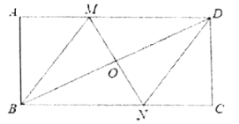
【答案】见解析
【解析】
根据MN是BD的垂直平分线可得OB=OD,根据两直线平行,内错角相等可得∠OBN=∠ODM,然后利用“角边角”证明△BON和△DOM全等,根据全等三角形对应边相等可得BN=MD,从而求出四边形BMDN是平行四边形,再根据线段垂直平分线上的点到两端点的距离相等可得MB=MD,然后根据邻边相等的平行四边形是菱形证明即可.
∵MN是BD的垂直平分线,
∴OB=OD,∠BON=∠DOM,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠OBN=∠ODM
在△BON和△DOM中,
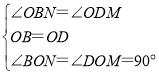 ,
,
∴△BON≌△DOM(ASA),
∴BN=MD,
∴四边形BMDN是平行四边形,
∵MN是BD的垂直平分线,
∴MB=MD,
∴平行四边形BMDN是菱形.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目