题目内容
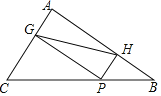
【题目】如图,在△ABC中,AC=9,AB=12,BC=15,P为BC边上一动点,PG⊥AC于点G,PH⊥AB于点H.
(1)求证:四边形AGPH是矩形;
(2)在点P的运动过程中,GH的长度是否存在最小值?若存在,请求出最小值,若不存在,请说明理由.
【答案】(1)证明见解析;(2)见解析.
【解析】
(1)根据“矩形的定义”证明结论;
(2)连结AP.当AP⊥BC时AP最短,结合矩形的两对角线相等和面积法来求GH的值.
(1)证明∵AC=9AB=12BC=15,
∴AC2=81,AB2=144,BC2=225,
∴AC2+AB2=BC2,
∴∠A=90°.
∵PG⊥AC,PH⊥AB,
∴∠AGP=∠AHP=90°,
∴四边形AGPH是矩形;
(2)存在.理由如下:
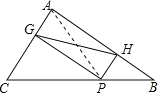
连结AP.
∵四边形AGPH是矩形,
∴GH=AP.
∵当AP⊥BC时AP最短.
∴9×12=15AP.
∴AP=![]() .
.

练习册系列答案
相关题目