题目内容
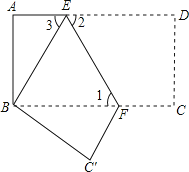
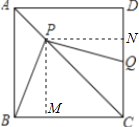
【题目】如图,正方形ABCD,点P是对角线AC上一点,连结BP,过P作PQ⊥BP,PQ交CD于Q,若AP=4![]() ,CQ=10,则正方形ABCD的面积为 .
,CQ=10,则正方形ABCD的面积为 .

【答案】324
【解析】
试题分析:作PM⊥BC于点M,PN⊥CD于点N,利用正方形的性质和角平分线上的点到角的两边相等以及已知条件即可证明△BPM≌△QPN,得出BM=QN,设BM=x,则NF=x,PM=CM=CN=10+x,根据平行线分线段成比例定理即可得到关于x的比例式,求出x的值,即可求出正方形的边长,进而求出其面积.
解:作PM⊥BC于点M,PN⊥CD于点N,如图所示:
∵四边形ABCD是正方形,
∴AC平分∠BCD,
∴PM=PN,∠NEM=90°,
∴四边形PMCN为正方形,∵PQ⊥BP,∴∠BPQ=90°,
∴∠BPM=∠NPQ,
在△BPM和△QPN中,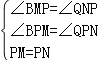 ,
,
∴△BPM≌△QPN(AAS),
∴BM=QN;
设BM=x,则NF=x,
∴PM=CM=CN=10+x,
∴CP=![]() (10+x),
(10+x),
∵PM∥AB,
∴![]() ,即
,即![]() ,
,
解得:x=4或x=﹣10(舍),
∴BM=4,CM=14,
∴BC=BM+CM=18,
∴正方形ABCD的面积为:18×18=324.
故答案为:324.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目