题目内容
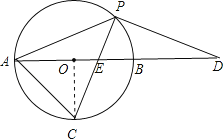
【题目】如图,以AB为直径的⊙O经过点P,C是⊙O上一点,连接PC交AB于点E,且∠ACP=60°,PA=PD.

(1)试判断PD与⊙O的位置关系,并说明理由;
(2)若![]() :
:![]() =1:2,求AE:EB:BD的值(请你直接写出结果);
=1:2,求AE:EB:BD的值(请你直接写出结果);
(3)若点C是弧AB的中点,已知AB=4,求CE![]() CP的值.
CP的值.
【答案】(1)PD与⊙O相切.理由见解析;(2)3:1:2(3)8
【解析】
试题分析:(1)连OP,根据圆周角定理得到∠AOP=2∠ACP=120°,则∠PAO=∠APO=30°,利用PA=PD得到∠D=∠PAD=30°,则∠APD=180°﹣30°﹣30°=120°,于是得到∠OPD=120°﹣30°=90°,根据切线的判定定理即可得到PD是⊙O的切线;
(2)连BC,由AB为直径,根据直径所对的圆周角为直角得到∠ACB=90°,利用![]() :
:![]() =1:2,则∠ABC=2∠BAC,所以有∠BAC=30°,∠ABC=60°,而∠PAE=30°,得到AE垂直平分PC,设BE=x,然后利用含30°的直角三角形三边的关系可求出AE:EB:BD的值;
=1:2,则∠ABC=2∠BAC,所以有∠BAC=30°,∠ABC=60°,而∠PAE=30°,得到AE垂直平分PC,设BE=x,然后利用含30°的直角三角形三边的关系可求出AE:EB:BD的值;
(3)根据圆周角定理由弧AC=弧BC,得到∠CAB=∠APC,OC⊥AB,根据相似三角形的判定方法易得△ACE∽△PCA,则![]() ,即AC2=PC
,即AC2=PC![]() CE,利用勾股定理有A02+OC2=AC2=8,即可得到CE
CE,利用勾股定理有A02+OC2=AC2=8,即可得到CE![]() CP的值.
CP的值.
解:(1)PD与⊙O相切.理由如下:
连接OP,
∵∠ACP=60°,
∴∠AOP=120°,
而OA=OP,
∴∠PAO=∠APO=30°,
∵PA=PD,
∴∠D=∠PAD=30°,
∴∠APD=180°﹣30°﹣30°=120°,
∴∠OPD=120°﹣30°=90°,
∵OP为半径,
∴PD是⊙O的切线;
(2)连BC,
∵AB为直径,
∴∠ACB=90°,
∵![]() :
:![]() =1:2,
=1:2,
∴∠ABC=2∠BAC,
∴∠BAC=30°,∠ABC=60°,
而∠PAE=30°,
∴∠APE=∠DPE=60°,
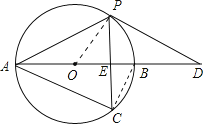
∴AE垂直平分PC,如图,
设BE=x,在Rt△BCE中,∠BCE=30°,则BC=2BE=2x,
在Rt△ABC中,∠CAB=30°,AB=2BC=4x,
∴AE=AB﹣BE=3x,
∵PA=PD,PE⊥AD,
∴AE=DE,
∴DB=3x﹣x=2x,
∴AE:EB:BD的值为3:1:2;
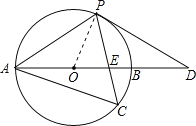
(3)如图,连接OC,
∵弧AC=弧BC,CO⊥AD,
∴∠CAB=∠APC,OC⊥AB,
而∠ACE=∠PCA,
∴△ACE∽△PCA,
∴![]() ,即AC2=PC
,即AC2=PC![]() CE,
CE,
∵A02+OC2=AC2=8,
∴PC![]() CE=AC2=8.
CE=AC2=8.

 优加精卷系列答案
优加精卷系列答案