题目内容
【题目】某商店今年1﹣6月份经营A、B两种电子产品，已知A产品每个月的销售数量y（件）与月份x（1≤x≤6且x为整数）之间的关系如表今年1﹣6月份经营A、B两种电子产品，已知A产品 每个月的销售数量y（件）与月份x（1≤x≤6且x为整数）之间的关系如表
x 1 2 3 4 5 6
y 600 300 200 150 120 100
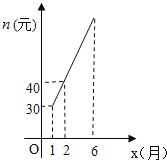
A产品每个月的售价z（元）与月份x之间的函数关系式为：z=10x，已知B产品每个月的销售数量m（件）与月份x之间的关系为：m=﹣2x+62，B产品每个月的售价n（元）与月份x存在如图所示的变化趋势．
（1）请观察题中表格，用所学过的一次函数或反比例函数的有关知识，直接写出y与x的函数关系式
（2）请观察如图所示的变化趋势，求出n与x的函数关系式
（3）求出此商店1﹣6月份经营A、B两种电子产品的销售总额w与月份x之间的函数关系式
（4）今年7月份，商店调整了A、B两种电子产品产品的价格，A产品价格在6月份基础上增加a%，B产品价格在6月份基础上减少a%，结果7月份A产品的销售数量比6月份减少2a%，B产品的销售数量比6月份增加2a%，若调整价格后7月份的销售总额比6月份的销售总额少2000元，请根据以下参考数据估算a的值．（参考数据：6.32=39.69，6.42=40.91，6.52=42.25，6.62=43.56）
【答案】（1）y=
（2）n=10x+20（3）w=﹣20x2+580x+7240（4）27
【解析】
试题分析：（1）根据图表中600×1=600，300×2=600…，得出此函数是反比例函数，k=600，即可得出答案；
（2）由图象可以列出函数解析式，设n=kx+b，代入两点解得k、b，即可得出解析式；
（3）利用销售总额w与y，z，m，n，之间的关系，即可得出月份x之间的函数关系式；
（4）根据6月份A产品的售价以及6月份B产品的售价，得出6月份B产品的销售数量，进而求出a%的值，分析得出a的值．
解：（1）y=；
（2）令n=kx+b（k≠0），
∵n=kx+b（k≠0）过（1，30），（2，40）
∴
，
∴
，
∴n=10x+20；
（3）利用销售总额w与y，z，mn，之间的关系，即可得出月份x之间的函数关系式；
W=yz+mn=
×10x+（﹣2x+62）（10x+20）
=6000+（﹣20x2+580x+1240），
=﹣20x2+580x+7240；
（4）今年6月份A产品的售价：z=10×6=60元
今年6月份B产品的售价：n=10×6+20=80元
今年6月份B产品的销售数量：
m=﹣2×6+62=50件，
60（1+a%）×100（1﹣2a%）+80（1﹣a%）×50（1+2a%），
=60×100+50×80﹣2000，
令p=a%，整理得10p2+p﹣1=0，
∴p1=
，p2=
（舍去）
∵6.32=39.69，6.42=40.91，6.52=42.25而40.91更接近41，
∴
≈6.4，
∴p
，
∴a≈27，
∴a的值约为27．
