题目内容
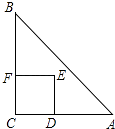
【题目】如图，在Rt△ABC中，∠ABC=90°，AC的垂直平分线分别与AC，BC及AB的延长线相交于点D，E，F，且BF=BC．⊙O是△BEF的外接圆，∠EBF的平分线交EF于点G，交⊙O于点H，连接BD，FH．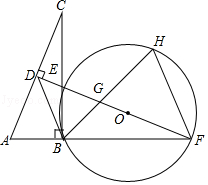 
（1）求证：△ABC≌△EBF；
（2）试判断BD与⊙O的位置关系，并说明理由；
（3）若AB=1，求HGHB的值．
【答案】
（1）证明：∵DF⊥AC，△ABC为Rt△，
∴∠CDE=∠EBF=90°
∵∠CED=∠FEB，
∴∠DCE=∠EFB，
在△ABC和△EBF中，
，
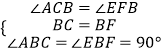∴△ABC≌△EBF，（ASA）
（2）解：结论：BD与⊙O相切．
理由：连接OB，
∵DF是AB的中垂线，∠ABC=90°，
∴DB=DC=DA，
∴∠DBC=∠C．
由（1）∠DCB=∠EFB，而∠EFB=∠OBF，
∴∠DBC=∠OBF，
∴∠DBO=∠DBC+∠EBO=∠OBF+∠EBO=90°，
∴DB⊥OB，
∴BD与⊙O相切
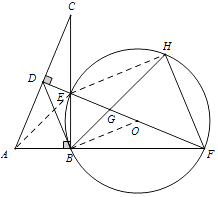
（3）解：连接EH，
∵BH是∠EBF的平分线，
∴∠EBH=∠HBF=45°．∠HFE=∠HBE=45°．
又∠GHF=∠FHB，
∴△GHF∽△FHB，
∴ 
= 
，
∴HGHB=HF2，
∵⊙O是Rt△BEF的内接圆，
∴EF为⊙O的直径，
∴∠EHF=90°，
又∠HFE=45°，
∴EH=HF，
∴EF2=EH2+HF2=2HF2，
在Rt△ABC中，AB=1，tan∠C= 
，
∴BC=2，AC= 
，
由（1）知△ABC≌△EBF，
∴EF=AC= 
，
∴2HF2=EF2=5，
∴HF2= 
，
故HGHB=HF2=
【解析】（1）根据ASA或AAS即可证明；（2）结论：BD与⊙O相切． 连接OB，只要证明OB⊥BD即可；（3）连接EH，首先证明△GHF∽△FHB，可得 = ，即HGHB=HF2 ， 想办法求出HF2即可解决问题．
