Question

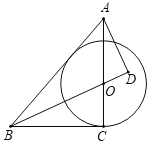
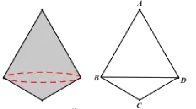
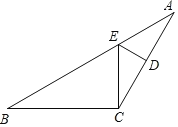
【题目】如图，在等腰△ABC中，AC=BC，∠ACB=4∠B，点D是AC边的中点，DE⊥AC，交AB于点E，连接CE．

（1）求∠BCE的度数；

（2）求证：AB=3CE．

Answer 1

【答案】（1）90°；（2）证明见解析．

【解析】

（1）证明△ECD≌△EAD，可得∠A=∠ECD，设∠B=x，可得∠BEC=2x，得出x+2x+3x=180°，解得x=30°，则∠BCE可求出；
（2）由直角三角形的性质可得BE=2CE，AE=CE，则结论可得出．

解:（1）∵点D是AC边的中点，DE⊥AC，

∴∠EDC=∠EDA=90°，DC=DA．

∵ED=ED，

∴△ECD≌△EAD（SAS），

∴∠A=∠ECD，

∵AC=BC，

∴∠B=∠A．

设∠B=x，

∴∠BEC=∠A+∠ECA=2x．

∵∠ACB=4∠B，

∴∠BCE=3x．

∵∠B+∠BEC+∠BCE=180°，

∴x+2x+3x=180°，

解得：x=30°，

∴∠BCE=90°；

（2）∵∠B=30°，∠BCE=90°，

∴BE=2CE．

∵CE=AE，

∴AB=BE+AE=3CE．