题目内容
【题目】已知抛物线![]() .
.
(1)当![]() ,
,![]() 时,求抛物线
时,求抛物线![]() 与
与![]() 轴的交点个数;
轴的交点个数;
(2)当![]() 时,判断抛物线
时,判断抛物线![]() 的顶点能否落在第四象限,并说明理由;
的顶点能否落在第四象限,并说明理由;
(3)当![]() 时,过点
时,过点![]() 的抛物线
的抛物线![]() 中,将其中两条抛物线的顶点分别记为
中,将其中两条抛物线的顶点分别记为![]() ,
,![]() ,若点
,若点![]() ,
,![]() 的横坐标分别是
的横坐标分别是![]() ,
,![]() ,且点
,且点![]() 在第三象限.以线段
在第三象限.以线段![]() 为直径作圆,设该圆的面积为
为直径作圆,设该圆的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)抛物线![]() 与
与![]() 轴有两个交点;(2)抛物线
轴有两个交点;(2)抛物线![]() 的顶点不会落在第四象限,理由详见解析;(3)
的顶点不会落在第四象限,理由详见解析;(3)![]() .
.
【解析】
(1)将![]() ,
,![]() 代入解析式,然后求当y=0时,一元二次方程根的情况,从而求解;(2)首先利用配方法求出顶点坐标,解法一:假设顶点在第四象限,根据第四象限点的坐标特点列不等式组求解;解法二:设
代入解析式,然后求当y=0时,一元二次方程根的情况,从而求解;(2)首先利用配方法求出顶点坐标,解法一:假设顶点在第四象限,根据第四象限点的坐标特点列不等式组求解;解法二:设![]() ,
,![]() ,则
,则![]() ,分析一次函数图像所经过的象限,从而求解;(3)将点
,分析一次函数图像所经过的象限,从而求解;(3)将点![]() 代入抛物线,求得a的值,然后求得抛物线解析式及顶点坐标,分别表示出A,B两点坐标,并根据点A位于第三象限求得t的取值范围,利用勾股定理求得
代入抛物线,求得a的值,然后求得抛物线解析式及顶点坐标,分别表示出A,B两点坐标,并根据点A位于第三象限求得t的取值范围,利用勾股定理求得![]() 的函数解析式,从而求解.
的函数解析式,从而求解.
解:(1)依题意,将![]() ,
,![]() 代入解析式
代入解析式
得抛物线![]() 的解析式为
的解析式为![]() .
.
令![]() ,得
,得![]() ,
,![]() ,
,
∴抛物线![]() 与
与![]() 轴有两个交点.
轴有两个交点.
(2)抛物线![]() 的顶点不会落在第四象限.
的顶点不会落在第四象限.
依题意,得抛物线![]() 的解析式为
的解析式为![]() ,
,
∴顶点坐标为![]() .
.
解法一:不妨假设顶点坐标在第四象限,
则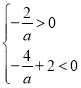 ,解得
,解得![]() .
.
∴该不等式组无解,
∴假设不成立,即此时抛物线![]() 的顶点不会落在第四象限.
的顶点不会落在第四象限.
解法二:设![]() ,
,![]() ,则
,则![]() ,
,
∴该抛物线![]() 的顶点在直线
的顶点在直线![]() 上运动,而该直线不经过第四象限,
上运动,而该直线不经过第四象限,
∴抛物线![]() 的顶点不会落在第四象限.
的顶点不会落在第四象限.
(3)将点![]() 代入抛物线
代入抛物线![]() :
:![]() ,
,
得![]() ,
,
化简,得![]() .
.
∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
∴此时,抛物线![]() 的解析式为
的解析式为![]() ,
,
![]()
∴顶点坐标为![]() .
.
当![]() 时,
时,![]() ,∴
,∴![]() .
.
当![]() 时,
时,![]() ,∴
,∴![]() .
.
∵点![]() 在第三象限,∴
在第三象限,∴![]()
∴![]() .
.
又![]() ,
,![]() ,
,
∴点![]() 在点
在点![]() 的右上方,
的右上方,
∴![]() .
.
∵![]() ,
,
∴当![]() 时,
时,![]() 随
随![]() 的增大而增大,
的增大而增大,
∴![]() .
.
又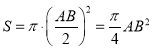 .
.
∵![]() ,
,
∴![]() 随
随![]() 的增大而增大,
的增大而增大,
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目