题目内容
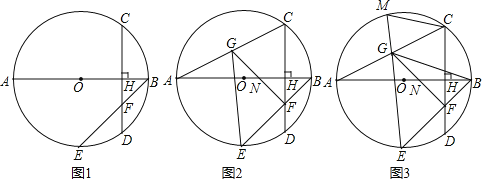
【题目】如图1,AB=AC=2,AD、BE为△ABC的两条高,F为AD上一点,且BD=DF,连接BF.
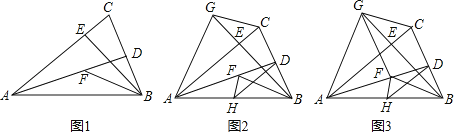
(1)求证:BF平分∠ABE;
(2)如图2,延长BE至G点,使BG=AB,连结GC,取AB的中点H,连结FH、DH.
求证:①△DFH∽△BCG;②若BF=CG,BF∥CG,连结GF,如图3,求AD的长.
【答案】(1)证明见解析;(2)①证明见解析;②![]() .
.
【解析】
(1)首先证明∠CBE=∠CAD=∠BAD,再证明∠ABF+∠BAD=∠EBF+∠CBE=45°即可解决问题.
(2)①根据两边对应成比例夹角相等的两个三角形相似即可证明.
②如图3中,连接CF交BG于O.证明四边形BFGC是平行四边形,△BFC是等腰直角三角形即可解决问题.
(1)如图1中,
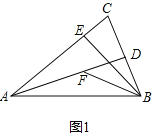
∵AD、BE为△ABC的两条高,
∴∠ADC=∠BEC=∠ADB=90°,
∴∠C+∠CAD=90°,∠C+∠CBE=90°,
∴∠CAD=∠CBE,
∵AC=AB,AD⊥BC,
∴∠CAD=∠BAD,
∴∠BAD=∠CBE,
∵DB=DE,∠BDF=90°,
∴∠DFB=∠DBF=45°,
∵∠DFB=∠FAB+∠FBA,∠DBF=∠CBE+∠EBF,
∴∠FAB+∠FBA=∠CBE+∠EBF,
∴∠ABF=∠EBF,
∴BF平分∠ABE;
(2)①如图2中,
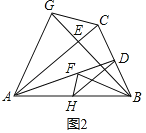
∵∠ADB=90°,AH=HB,
∴DH=AH=BH,
∴∠HAD=∠HDA,
∵∠BAD=∠CBE,
∴∠ADH=∠CBG,
∵![]() ,
,![]() =
=![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
②如图3中,连接CF交BG于O.
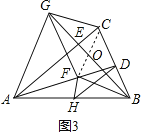
∵BF=CG,BF∥CG,
∴四边形BFGC是平行四边形,
∴OF=OC,OB=OG=1,
∵FD垂直平分线段BC,
∴FC=FB,
∵∠FBD=45°,
∴△BFC是等腰直角三角形,
∴BF=2OF,
∵OB=1,
![]() ,即
,即![]()
解得:![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,
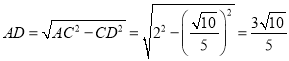 .
.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案