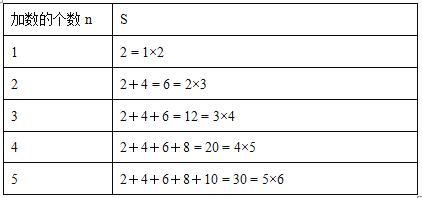题目内容
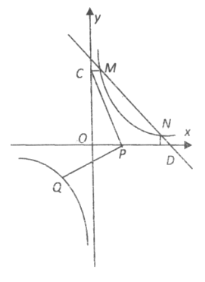
【题目】已知:如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于M,N两点,过点M作MC⊥y轴于点C,且CM=1,过点N作ND⊥x轴于点D,且DN=1,已知点P是x轴(除原点O外)上一点.
的图象交于M,N两点,过点M作MC⊥y轴于点C,且CM=1,过点N作ND⊥x轴于点D,且DN=1,已知点P是x轴(除原点O外)上一点.
(1)直接写出M、N的坐标及k的值;
(2)将线段CP绕点P按逆时针旋转90°得到线段PQ,当点P滑动时,点Q能否在反比例函数的图象上?如果能,求出点Q的坐标;如果不能,请说明理由;
(3)当点P滑动时,是否存在反比例函数图象(第一象限的一支)上的点S,使得以P、S、M、N四个点为顶点的四边形是平行四边形?若存在,请直接写出所有符合题意的点S的坐标;若不存在,请说明理由.
【答案】(1)![]() (2)
(2)![]() ;(3)存在,S的坐标为
;(3)存在,S的坐标为![]() 或
或![]() .
.
【解析】
(1)根据题意可得M点的横坐标为1,代入一次函数计算可得纵坐标,进而可得M点的坐标,已知N点的纵坐标,代入一次函数可得N点的横坐标,进而可得N点的坐标;
(2)设P点的坐标为(x,0),根据C、P可以计算出CP所在直线的解析式,进而可得PQ所在直线的解析式,就可以表示Q点的坐标,在代入反比例函数,即可求得x,从而可得Q点的坐标;
(3)根据P点的坐标,将四边形其余各点都表示出来,再代入反比例函数看是否有解,有解则说明此点存在,无解说明不存在,进而可得S点的坐标。
解:(1)当![]() 时,
时,![]() ,
,![]() .
.
当![]() 时,
时,![]() ,解得
,解得![]() ,
,
将点![]() 代入
代入![]() 得
得![]() ,
,
![]() ;
;
(2)若CP逆时针旋转,点Q在双曲线上,
设![]() ,则
,则![]() ,
,
![]() ,即
,即![]() ,
,
![]() ,
,
![]() ;
;
(3)设![]() ,
,
当MN为平行四边形的一条边时,则![]() ,
,
把S点的坐标代入![]() ,得
,得![]() ,解得
,解得![]() .
.
当MN为平行四边形的对角线时,则![]() ,
,
把S点的坐标代入![]() ,得
,得![]() ,解得
,解得![]() ,
,
∴存在,S的坐标为![]() 或
或![]() .
.

【题目】网上办公,手机上网已成为人们日常生活的一部分,我县某通信公司为普及网络使用,特推出以下两种电话拨号上网收费方式,用户可以任选其一.
收费方式一(计时制):0.05元/分;
收费方式二(包月制):50元/月(仅限一部个人电话上网);
同时,每一种收费方式均对上网时间加收0.02元/分的通信费.
某用户一周内的上网时间记录如下表:
日期 | 上网时间(分钟) |
星期一 | 35 |
星期二 | 40 |
星期三 | 33 |
星期四 | 50 |
星期五 | 34 |
星期六 | 40 |
星期日 | 48 |
(1)计算该用户一周内平均每天上网的时间.
(2)设该用户12月份上网的时间为![]() 小时,请你分别写出两种收费方式下该用户所支付的费用. (用含
小时,请你分别写出两种收费方式下该用户所支付的费用. (用含![]() 的代数式表示)
的代数式表示)
(3)如果该用户在一个月(30天)内,按(1)中的平均每天上网时间计算,你认为采用哪种方式支付费用较为合算?并说明理由.