题目内容
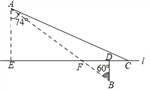
【题目】如图，在航线l的两侧分别有观测点A和B，点B到航线l的距离BD为4km，点A位于点B北偏西60°方向且与B相距20km处．现有一艘轮船从位于点A南偏东74°方向的C处，沿该航线自东向西航行至观测点A的正南方向E处．求这艘轮船的航行路程CE的长度．（结果精确到0.1km）（参考数据：
≈1.73，sin74°≈0.96，cos74°≈0.28，tan74°≈3.49）
【答案】20.9km
【解析】分析：根据题意，构造直角三角和相似三角形的数学模型，利用相似三角形的判定与性质和解直角三角形即可.
详解：如图，
在Rt△BDF中，∵∠DBF=60°，BD=4km，
∴BF=
=8km，
∵AB=20km，
∴AF=12km，
∵∠AEB=∠BDF，∠AFE=∠BFD，
∴△AEF∽△BDF，
∴
，
∴AE=6km，
在Rt△AEF中，CE=AEtan74°≈20.9km．
故这艘轮船的航行路程CE的长度是20.9km．
练习册系列答案
阳光课堂同步练习系列答案
相关题目
