Question

【题目】在等腰直角三角形ABC中,∠ACB＝90°,AC＝BC,D是AB边上的中点，Rt△EFG的直角顶点E在AB边上移动.

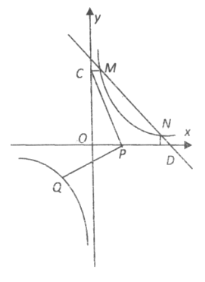
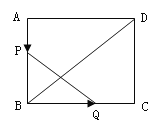
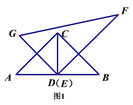
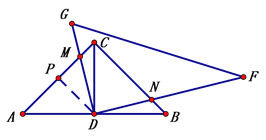
(1)如图1，若点D与点E重合且EG⊥AC、DF⊥BC，分别交AC、BC于点M、N，

易证EM＝EN；如图2，若点D与点E重合，将△EFG绕点D旋转，则线段EM与EN的长度还相等吗?若相等请给出证明，不相等请说明理由；

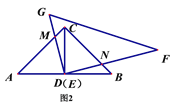
(2)将图1中的Rt△EGF绕点O顺时针旋转角度α(0＜α＜45). 如图2，在旋转过程中,当∠MDC＝15时，连接MN，若AC＝BC＝2，请求出写出线段MN的长；

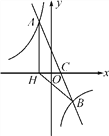
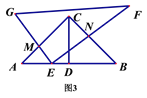
(3) 图3, 旋转后,若Rt△EGF的顶点E在线段AB上移动(不与点D、B重合)，当AB＝3AE时，线段EM与EN的数量关系是________；当AB＝m·AE时，线段EM与EN的数量关系是__________.

Answer 1

【答案】 NE＝2ME EN＝(m－1)ME

【解析】分析：（1）易证△CDM≌△BDN，从而得出DM＝DN 即EM＝EN；

（2）作DP⊥AC于P,通过解直角三角形DPM得出DM=，由△MND为等腰直角三角形得出结论；

（3）过点E作EP⊥AB交AC于点P，则△AEP为等腰直角三角形，通过证明△PME∽△BNE，得到EN＝2EM，由此规律可知，当AB＝m·AE时，EN＝(m－1)·ME

详解：（1）EM＝EN;原因如下：

∵∠ACB＝90° AC＝BC D是AB边上的中点

∴DC＝DB ∠ACD＝∠B＝45° ∠CDB＝90°

∴∠CDF＋∠FDB＝90°

∵∠GDF＝90°∴∠GDC＋∠CDF＝90°∴∠CDM＝∠BDN

在△CDM和△BDN中

∠MCD＝∠B，DC＝DB，∠CDM＝∠BDN，

∴△CDM≌△BDN ∴DM＝DN 即EM＝EN

(2)作DP⊥AC于P,则

∠CDP＝45° CP＝DP＝AP＝1

∵∠CDG＝15° ∴∠MDP＝30°

∵cos∠MDP＝

∴DM＝， DM＝DN，

∵△MND为等腰直角三角形

∴MN＝

(3)NE＝2ME,EN＝(m－1)ME

证明：如图3，过点E作EP⊥AB交AC于点P

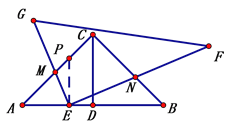
则△AEP为等腰直角三角形，∠PEB＝90°

∴AE＝PE ∵AB＝3AE ∴BE＝2AE ∴BE＝2PE

又∵∠MEP＋∠PEN＝90°

∠PEN＋∠NEB＝90°

∴∠MEP＝∠NEB

又∵∠MPE＝∠B＝45°

∴△PME∽△BNE

∴，即EN＝2EM

由此规律可知，当AB＝m·AE时，EN＝(m－1)·ME