题目内容
【题目】如图,二次函数Y=-![]() x2-
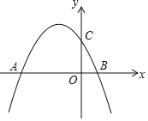
x2-![]() x+2图象与x轴交于A、B两点,与y轴交于C点,点D(m,n)是抛物线在第二象限的部分上的一动点,则四边形OCDA的面积的最大值是______.
x+2图象与x轴交于A、B两点,与y轴交于C点,点D(m,n)是抛物线在第二象限的部分上的一动点,则四边形OCDA的面积的最大值是______.
【答案】8
【解析】
根据解析式求得点A、C坐标,过点D作DH⊥x轴于点H,运用割补法即可得到:四边形OCDA的面积=△ADH的面积+四边形OCDH的面积,据此列式计算化简就可求得S关于m的函数关系,配方成顶点式可得其最值情况.
解:在y=-![]() x2-
x2-![]() x+2中,当x=0时,y=2,
x+2中,当x=0时,y=2,
∴C(0,2),
当y=0时,有-![]() x2-
x2-![]() x+2=0,解得:x=-4或x=1,
x+2=0,解得:x=-4或x=1,
∴点A(-4,0)、B(1,0),
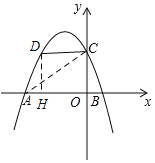
∵点D(m,n)是抛物线在第二象限的部分上的一动点,
∴D(m,-![]() m2-
m2-![]() m+2),
m+2),
过点D作DH⊥x轴于点H,则DH=-![]() m2-
m2-![]() m+2,AH=m+4,HO=-m,
m+2,AH=m+4,HO=-m,
∵四边形OCDA的面积=△ADH的面积+四边形OCDH的面积,
∴S=![]() (m+4)×(-
(m+4)×(-![]() m2-
m2-![]() m+2)+
m+2)+![]() (-
(-![]() m2-
m2-![]() m+2+2)×(-m),
m+2+2)×(-m),
=-m2-4m+4
=-(m+2)2+8,(-4<m<0);
则m=-2时,S取得最大值,最大值为8,

练习册系列答案
相关题目