题目内容
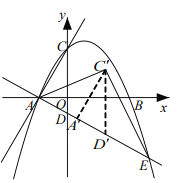
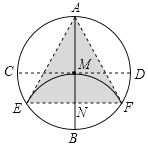
【题目】李老师是我区“IDJP”课题研究的主要成员之一,一天他在视频微课中提出了以下问题:如图,AB,CD为圆形纸片中两条互相垂直的直径,将圆形纸片沿EF折叠,使B与圆心M重合,折痕EF与AB相交于N连结AE,AF.李老师提出两个猜想和一个问题,请你证明或解答出来:
①四边形MEBF是菱形;
②△AEF为等边三角形;
③求S△AEF:S圆.
【答案】(1)见解析;(2)见解析;(3)S△AEF:S圆=3![]() :4π.
:4π.
【解析】
①由折叠的性质可得出BN=MN,∠BNF=∠MNF,结合∠BNF+∠MNF=180°可得出BM⊥EF,由垂径定理可得出EN=FN,由BN,EF互相平分可得出四边形MEBF是平行四边形,再由BN⊥EF可证出四边形MEBF是菱形;
②由菱形的性质可得出∠EBF=∠EMF,由圆周角定理及圆内接四边形的性质可求出∠EAF=60°,由AN=AN,∠ANE=∠ANF,EN=FN可得出△AEN≌△AFN(SAS),利用全等三角形的性质可得出AE=AF,结合∠EAF=60°可证出△AEF为等边三角形;
③设圆M的半径为r,则AN=![]() r,EF=
r,EF=![]() r,利用三角形及圆的面积公式可求出S△AEF,S圆的值,进而可求出S△AEF:S圆的值.
r,利用三角形及圆的面积公式可求出S△AEF,S圆的值,进而可求出S△AEF:S圆的值.
①证明:由折叠的性质可知:BN=MN,∠BNF=∠MNF,
∵∠BNF+∠MNF=180°,
∴∠BNF=90°,即BM⊥EF.
∵点M为圆心,EF为⊙M的弦,BM⊥EF,
∴EN=FN,
∴四边形MEBF为平行四边形,
又∵BN⊥EF,
∴四边形MEBF是菱形;

②证明:由①可知:∠EBF=∠EMF.
∵∠EMF=2∠EAF,∠EBF+∠EAF=180°,
∴∠EAF=60°.
在△AEN和△AFN中,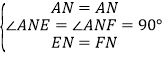 ,
,
∴△AEN≌△AFN(SAS),
∴AE=AF,
∴△AEF为等边三角形;
③解:设圆M的半径为r,则AM=MF=r,MN=![]() r,FN=
r,FN=![]() =
=![]() r,
r,
∴EF=2FN=![]() r,
r,
∴S△AEF=![]() EFAN=
EFAN=![]() r2.
r2.
∴S圆=πr2,
∴S△AEF:S圆=3![]() :4π.
:4π.

【题目】(9分)某市球类运动协会为了筹备一次大型体育活动,购进了一定数量的体育器材,器材管理员对购买的部分器材进行了统计,表1和图2是器材管理员通过采集数据后,绘制的两幅不完整的频率分布表与频数分布直方图.请你根据图表中提供的信息,解答以下问题:
频率分布表
器材种类 | 频数 | 频率 |
排 球 | 20 | |
乒乓球拍 | 50 | 0.50 |
篮 球 | 25 | 0.25 |
足 球 | ||
合 计 | 1 |
![]()
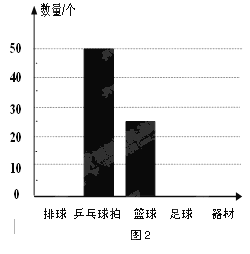
(1)填充图1频率分布表中的空格.
(2)在图2中,将表示“排球”和“足球”的部分补充完整.
(3)已知该协会购买这批体育器材时,篮球和足球一共花去950元,且足球每个的价格比篮球多10元.现准备再采购篮球和足球这两种球共10个(两种球的个数都不能为0),计划资金不超过320元,试问该协会有哪几种购买方案?