题目内容
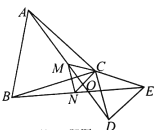
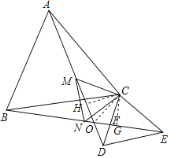
【题目】如图,△ABC、△CDE都是等腰三角形,且CA=CB,CD=CE,∠ACB=∠DCE=α,AD,BE相交于点O,点M,N分别是线段AD,BE的中点,以下4个结论:①AD=BE;②∠DOB=180°-α;③△CMN是等边三角形;④连OC,则OC平分∠AOE.正确的是( )
A.①②③B.①②④C.①③④D.①②③④
【答案】B
【解析】
①根据全等三角形的判定定理得到△ACD≌△BCE(SAS),由全等三角形的性质得到AD=BE;故①正确;
②设CD与BE交于F,根据全等三角形的性质得到∠ADC=∠BEC,得到∠DOE=∠DCE=α,根据平角的定义得到∠BOD=180°-∠DOE=180°-α,故②正确;
③根据全等三角形的性质得到∠CAD=∠CBE,AD=BE,AC=BC根据线段的中点的定义得到AM=BN,根据全等三角形的性质得到CM=CN,∠ACM=∠BCN,得到∠MCN=α,推出△MNC不一定是等边三角形,故③不符合题意;
④过C作CG⊥BE于G,CH⊥AD于H,根据全等三角形的性质得到CH=CG,根据角平分线的判定定理即可得到OC平分∠AOE,故④正确.
解:①∵CA=CB,CD=CE,∠ACB=∠DCE=α,
∴∠ACB+∠BCD=∠DCE+∠BCD,
∴∠ACD=∠BCE,
在△ACD和△BCE中

∴△ACD≌△BCE(SAS),
∴AD=BE;故①正确;
②设CD与BE交于F,
∵△ACD≌△BCE,
∴∠ADC=∠BEC,
∵∠CFE=∠DFO,
∴∠DOE=∠DCE=α,
∴∠BOD=180°-∠DOE=180°-α,故②正确;
③∵△ACD≌△BCE,
∴∠CAD=∠CBE,AD=BE,AC=BC
又∵点M、N分别是线段AD、BE的中点,
∴AM=![]() AD,BN=
AD,BN=![]() BE,
BE,
∴AM=BN,
在△ACM和△BCN中
∴△ACM≌△BCN(SAS),
∴CM=CN,∠ACM=∠BCN,
又∠ACB=α,
∴∠ACM+∠MCB=α,
∴∠BCN+∠MCB=α,
∴∠MCN=α,
∴△MNC不一定是等边三角形,故③不符合题意;
④过C作CG⊥BE于G,CH⊥AD于H,
∴∠CHD=∠ECG=90°,∵∠CEG=∠CDH,CE=CD,
∴△CGE≌△CHD(AAS),
∴CH=CG,
∴OC平分∠AOE,故④正确,
故选:B.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案