Question

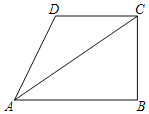
【题目】如图，在四边形ABCD中，AB∥CD，∠B＝90°，连接AC，∠DAC＝∠BAC．

（1）求证：AD＝DC；

（2）若∠D＝120°，求∠ACB的度数．

Answer 1

【答案】（1）见解析；（2）∠ACB＝60°

【解析】

（1）由平行线的性质可得∠DCA＝∠BAC＝∠DAC，可得AD＝DC；

（2）由平行线的性质可得∠DCB＝90°，由等腰三角形的性质可得∠ACD＝30°，即可求解．

证明：（1）∵AB∥CD，

∴∠DCA＝∠BAC，

∵∠DAC＝∠BAC，

∴∠DAC＝∠DCA，

∴AD＝DC；

（2）∵AB∥CD，

∴∠B+∠DCB＝180°，且∠B＝90°，

∴∠DCB＝90°，

∵AD＝DC，∠D＝120°，

∴∠ACD＝30°

∴∠ACB＝∠DCB﹣∠DCA＝60°．