Question

【题目】如图，在⊙O中，AB为直径，AC=5，AB=10，

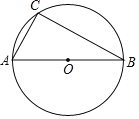
（1）作以AC为底边的圆内接等腰△ACD；（要求：尺规作图，不写作法，保留作图痕迹）

（2）求弦AC所对的圆周角。

Answer 1

【答案】（1）见解析；（2）30°或150°

【解析】

（1）作出AC的垂直平分线，与圆的交点即是三角形的顶点，有两种情况，连接即可得出答案；

（2）根据圆周角定理和圆内接四边形的性质即可得到结论．

（1）①作出AC的垂直平分线，与圆的交点D即是三角形的顶点，

②连接AD、DC即可得出，

如图所示；

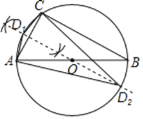
（2）在⊙O中，AB为直径，AC=5，AB=10，

∴∠ACB=90°，AC=AB，

∴∠B=30°，

∴∠AD2C=30°，

∴∠AD1C=180°-30°=150°，

∴弦AC所对的圆周角为30°或150°．