Question

【题目】已知抛物线y=ax2+bx+c过点A（0,2）。

（1）若点（-，0）也在该抛物线上，求a，b满足的关系式；

（2）若点A为抛物线顶点，且抛物线过点（1,1）。

①求抛物线的解析式；

②若点M是抛物线上异于点A的一个动点，点P与点O关于点A对称，直线MP交抛物线与另一个点N，点N’是抛物线上点N关于对称轴的对称点，直线PN’与抛物线交于点E，求证：直线EN恒过点O。

Answer 1

【答案】（1）3a-b=-2；（2）①y=-+2，②见解析

【解析】

（1）由抛物线经过点A可求出c=2，再代入（-，0）即可找出3a-b=-2（a≠0）；

（2）由A点为抛物线的顶点，可设y=ax2+2，把（1，1）代入求出a的值即可；

（3）设M点的坐标为（m，m2+2）求出直线PM的解析式，与抛物线方程联立，求出N点坐标，根据M点与E点关于y轴对称求出E点坐标，从而求出直线EN的解析式，判断当x=0时，y=0即可.

（1）∵抛物线y=ax2+bx+c过点A（0，2），

∴c=2．

又∵点（-，0）也在该抛物线上，

∴a（-）2+b（-）+c=0，

∴3a-b+2=0（a≠0）．

即3a-b=-2；

（2）∵点A（0，2）是抛物线的顶点坐标，

∴设，

∵函数的图象经过（1，1）

∴1=a+2，解得，a=-1，

∴抛物线的解析式为：

（3）设M点的坐标为（m，-m2+2）(m＜0），

设直线PM的解析式为：

∵点P与点O关于点A对称，A（0，2），

∴P（0，4），

∴，

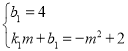解得，，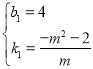

∴直线PM的解析式为：，

联立方程组得，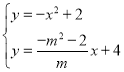

解得，，，

∴N（，）.

∵M点与E点关于y轴对称,

∴E(-m，-m2+2)

设直线NE的解析式为：，

将N点、E点坐标代入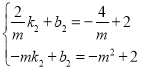得，，解得，

∴直线EN的解析式为：

∴当x=0时，y=0，

∴直线EN恒过点O.