题目内容
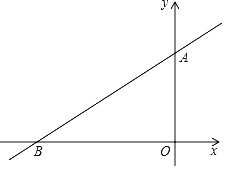
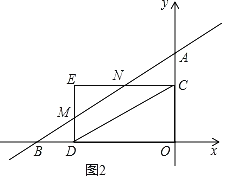
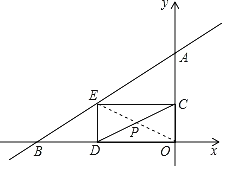
【题目】如图,在平面直角坐标系中,直线![]() 与x轴、y轴分别相交于点A,B,点C在射线OA上,点D在射线OB上,且OD=2OC,以CD的中点为对称中心作△COD的对称图形△DEC.设点C的坐标为(0,n),△DEC在直线AB下方部分的面积为S.
与x轴、y轴分别相交于点A,B,点C在射线OA上,点D在射线OB上,且OD=2OC,以CD的中点为对称中心作△COD的对称图形△DEC.设点C的坐标为(0,n),△DEC在直线AB下方部分的面积为S.
(1)当点E在AB上时,n= ,当点D与点B重合时,n= ;
(2)求S关于n的函数解析式,并直接写出自变量n的取值范围.
【答案】(1)![]() ;2;(2)
;2;(2)![]()
【解析】
(1)根据题意证得四边形DOCE是矩形,即可得到E(-2n,n),D(-2n,0),由直线上点的坐标特征求得n的值即可;
(2)分两种情况讨论:①当直线AB经过线段DE时,求得直线与DE和EC的交点坐标,进而求得△MEN的面积,则根据S=S△EDC-S△EMN即可求得S关于n的函数解析式;②当直线AB经过线段DC时,求得直线与DC的交点,然后根据三角形面积公式即可求得.
解:(1)设点C的坐标为(0,n),则D(﹣2n,0),
∵△COD与△DEC关于P点成中心对称,
∴PD=PC,PE=PO,
∴四边形DOCE是平行四边形,
∵∠DOC=90°,
∴四边形DOCE是矩形,
∴E(﹣2n,n),
点E在AB上时,则n=![]() (﹣2n)+3,
(﹣2n)+3,
解得n=![]() ;
;
当点D与点B重合时,则0=![]() (﹣2n)+3,
(﹣2n)+3,
解得n=2,
故答案为![]() ,2;
,2;
(2)如图2,当直线AB经过线段DE时,
把x=﹣2n代入y=![]() x+3得y=﹣
x+3得y=﹣![]() n+3,把y=n代入y=
n+3,把y=n代入y=![]() x+3求得x=
x+3求得x=![]() n﹣4,
n﹣4,
∴M(﹣2n,﹣![]() n+3),N(
n+3),N(![]() n﹣4,n),
n﹣4,n),
∴S△EMN=![]() (n+
(n+![]() n﹣3)(
n﹣3)(![]() n﹣4+2n)
n﹣4+2n)
∴S=S△EDC﹣S△EMN=![]() 2
2![]() (n+
(n+![]() n﹣3)(
n﹣3)(![]() n﹣4+2n)=﹣
n﹣4+2n)=﹣![]() n2+10n﹣6(
n2+10n﹣6(![]() ≤n≤2),
≤n≤2),
当直线AB经过线段DC时,
∵OD=2OC,
∴直线DC的解析式为y=![]() x+n,
x+n,
解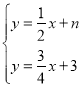 得
得![]() ,
,
∴S=![]() (
(![]() n﹣4)(6﹣2n)=﹣
n﹣4)(6﹣2n)=﹣![]() n2+8n﹣12(2<n≤3).
n2+8n﹣12(2<n≤3).
综上,S=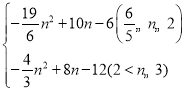 .
.

【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元[
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.