Question

【题目】如图，在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝6.点E从点A出发，沿AC以每秒1个单位长度的速度向终点C运动：点D从点C出发，沿C一B一A以每秒2个单位长度的速度向终点A运动，当点E停止运动时，点D随之停止，点E、D同时出发，设点E的运动时间为t(秒)

(1)用含t的代数式表示CE的长；

(2)设点D到CA的距离为h，用含t的代数式表示h；

(3)设△CDE的面积为S(平方单位)，求S(平方单位)与t(秒)的函数关系式；

(4)当DE与△ABC的边平行或垂直时，直接写出t的值.

Answer 1

【答案】(1)CE＝8﹣t；(2)h＝2t(0≤t≤3)，h＝﹣t+(3＜t≤8)；(3)S＝﹣t2+8t(0≤t≤3)，S＝t2﹣t+(3＜t≤8)；(4)t的值为s或s.

【解析】

(1)根据线段的和差定义求出AE即可解决问题.

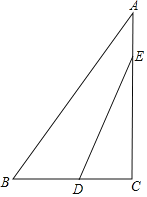
(2)分两种情形：①如图1中，当0≤t≤3时.②如图2，当3＜t≤8时，如图，作DH⊥AC于点H，分别求解即可.

(3)根据图1，图2中，两种情形分别求解即可解决问题.

(4)①如图1中，当0≤t≤3时，DE∥AB时，＝，由此构建方程即可解决问题.

②如图2，当3＜t≤8时，DE∥BC时，＝，由此构建方程即可解决问题.

(1)如图1，

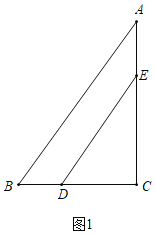
∵∠ACB＝90°，AC＝8，BC＝6，

∴AB＝＝＝10，

∵点E从点A出发，沿AC以每秒1个单位的速度向终点C运动，

∴AE＝t，

又∵AC＝8，

∴CE＝8﹣t.

(2)①如图1中，当0≤t≤3时，

∵点D从点C出发，沿C﹣B﹣A以每秒2个单位的速度向终点A运动，

∴h＝DC＝2t.

②如图2，当3＜t≤8时，如图，作DH⊥AC于点H，

，

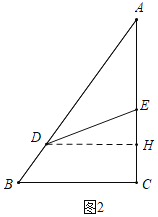∵sinA＝＝＝＝，

∴＝，

∴h＝﹣t+.

(3)①如图1中，当0≤t≤3时，S＝CDEC＝×2t×(8﹣t)＝﹣t2+8t.

②如图2，当3＜t≤8时，S＝DHEC＝×(﹣t+)×(8﹣t)＝t2﹣t+.

(4)①如图1中，当0≤t≤3时，DE∥AB时，＝，

∴＝，

解得t＝.

②如图2，当3＜t≤8时，DE∥BC时，＝，

∴＝，

解得t＝，

综上所述，满足条件的t的值为s或s.