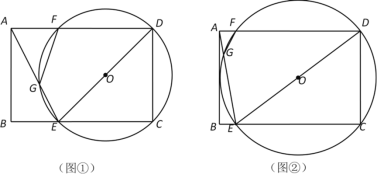题目内容
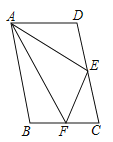
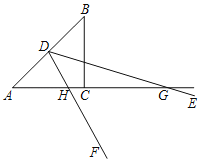
【题目】如图,在△![]() 中,高
中,高![]() =3,∠
=3,∠![]() =45°,
=45°,![]() =
=![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向以每秒1个单位长度的速速向终点
方向以每秒1个单位长度的速速向终点![]() 运动,当点
运动,当点![]() 与点
与点![]() 、
、![]() 不重合时,过点
不重合时,过点![]() 作
作![]() 、
、![]() 的平行线,与
的平行线,与![]() 分别交于点
分别交于点![]() 、
、![]() ,将△
,将△![]() 绕
绕![]() 的中点旋转180°得△
的中点旋转180°得△![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() 秒,△
秒,△![]() 与△
与△![]() 重叠部分面积为
重叠部分面积为![]() .
.
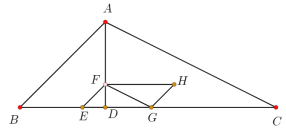
(1)当![]() = 秒时,点
= 秒时,点![]() 落在
落在![]() 边上.
边上.
(2)求![]() 与
与![]() 的函数关系式.
的函数关系式.
(3)当直线![]() 将△
将△![]() 分为面积比为1:3的两部分时,直接写出
分为面积比为1:3的两部分时,直接写出![]() 的值.
的值.
【答案】(1)![]() ;(2)当0<1≤
;(2)当0<1≤![]() 时,
时,![]() ;
;![]() <t<3时,S=
<t<3时,S=![]() ;(3)t=
;(3)t=![]() 或t=
或t=![]()
【解析】
(1)由旋转的性质可得EH=FG=3t,再根据平行线分线段成比例可得![]() ,得到方程求解即可;
,得到方程求解即可;
(2)分0<1≤![]() 和
和![]() <t<3时,结合图形利用三角形面积计算公式即可得出函数关系;
<t<3时,结合图形利用三角形面积计算公式即可得出函数关系;
(3)根据“直线![]() 将△
将△![]() 分为面积比为1:3的两部分”分两种情况由BG:BC=1:2与BG:BC=
分为面积比为1:3的两部分”分两种情况由BG:BC=1:2与BG:BC=![]() :2时求出t的值即可.
:2时求出t的值即可.
(1)当点H落在AC边上时,如图1,
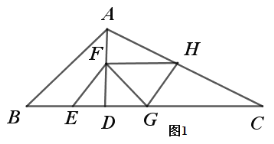
∵AD ⊥BC,∠B=45°
∴△ABD为等腰直角三角形,
∵FE// AB,
∴△FED为等腰直角三角形,
∴ED=FD=t,
又∵FG//AC,
∴∠FGD=∠C,
∴tan∠FGD=tan C=![]()
∴DG=2t,
∴EG=3t
又∵△HG由△EFG旋转得到,
FH=EG=3t, 四边形FE GH为平行四边形,
∴FH //BC,
∴![]()
∴![]() ,解得,t=
,解得,t=![]() ,
,
即当t=![]() 秒时,点H落在AC边上.
秒时,点H落在AC边上.
故答案为:![]() ;
;
(2) ①当0<1≤![]() 时, 如图2, 重叠部分图形为A HGF,
时, 如图2, 重叠部分图形为A HGF,
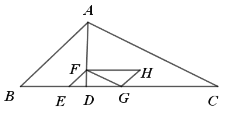
图2
∴![]()
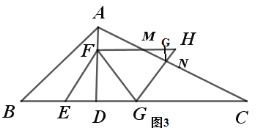
②当![]() <t<3时, 如图3,重叠部分图形为四边形MFG N,
<t<3时, 如图3,重叠部分图形为四边形MFG N,
![]() ,
,![]()
![]()
![]()
![]()
![]() ,
,
![]()
![]()
![]()
过N作![]() 于K,
于K,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
=![]()
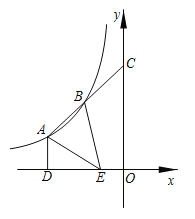
(3)①当BG:BC=1:2时, 如图4,

此时KG为△ABC的中位线,S△BKG:S四边形AKGC=1:3,
∵AD=3,∠ABD=45°,AD⊥BC
∴BD=AD=3,
∵KG//AC,
∴∠C=∠KGB,tanC=![]() ,
,
∴tan∠KGB =![]() ,
,
∴DG=2t,DC=6
∴BC=9,
∴![]() ,解得,t=
,解得,t=![]() ;
;
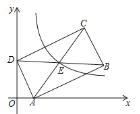
②当BG:BC=![]() :2时,如图5,此时S四边形AKGC:S△BKG=1:3,
:2时,如图5,此时S四边形AKGC:S△BKG=1:3,

∴![]() ,解得,t=
,解得,t=![]()
综上, 当直线FG将△ABC分为面积比为1:3的两部分时,t=![]() 或t=
或t=![]() .
.

【题目】某初中学校餐厅为了解学生对早餐的要求,随即抽样调查了该校的部分学生,并根据其中两个单选问题的调查结果,绘制了如下尚不完整的统计图表.
学生能接受的早餐价格统计表
价格分组(单位:元) | 频数 | 频率 |
0<x≤2 | 60 | 0.15 |
2<x≤4 | 180 | c |
4<x≤6 | 92 | 0.23 |
6<x≤8 | a | 0.12 |
x>8 | 20 | 0.05 |
合计 | b | 1 |
根据以上信息解答下列问题:
(1)统计表中,a= ,b= ,c= .
(2)扇形统计图中,m的值为 ,“甜”所对应的圆心角的度数是 .
(3)该餐厅计划每天提供早餐2000份,其中咸味大约准备多少份较好?