题目内容
【题目】如图,△ABC中,∠BAC的内角平分线与外角平分线分别交BC及BC的延长线于点P、Q.
(1)求∠PAQ的大小;
(2)若点M为PQ的中点,求证:PM2=CM·BM.
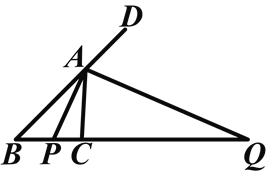
【答案】见解析
【解析】
(1)由角平分线的性质及∠BAD为平角直接可得;(2)由于线段PM、CM、BM在同一条直线上,所以必须把某条线段转化为另一相等的线段,构造相似三角形,因此,可证PM=AM,从而证明△ACM与△ABM相似即可.
解:
(1)∵AP平分∠BAC,∴![]() ,
,
又∵AQ平分∠CAD,∴![]() .
.
∴![]() .
.
又∵∠BAC+∠CAD=∠180°,∴∠PAC+∠CAQ=90°,即∠PAQ=90°.
(2)证明:如图,连接AM,∵∠PAQ=90°,M是PQ的中点,∴PM=AM,∴∠APM=∠PAM.
∵∠APM=∠B+∠BAP,∠PAM=∠CAM+∠PAC,
∴∠B=∠CAM,∵∠AMC=∠BMA,
∴△ACM∽△BAM.
∴![]() .∴AM2=CM·BM,即PM2=CM·BM.
.∴AM2=CM·BM,即PM2=CM·BM.


练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目