题目内容
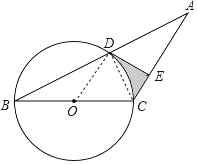
【题目】如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
(1)证明:DE为⊙O的切线;
(2)若BC=4,求阴影部分的面积.

【答案】(1)证明见解析(2)![]()
【解析】
(1)连接OD,CD,由以BC为直径的⊙O,可得∠BDC=90°,又由等腰△ABC的底角为30°,可得AD=BD,即可证得OD∥AC,继而可证得结论;(2)根据三角函数的性质,求得CD、CE、DE的长,根据S阴=S四边形ODEC﹣S扇形ODC即可求得阴影部分的面积.
(1)证明:连接OD,CD,
∵BC为⊙O直径,
∴∠BDC=90°,
∵△ABC是等腰三角形,
∴AD=BD,
∵OB=OC,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥DE,
∴DE为⊙O的切线;
(2)∵∠A=∠B=30°,BC=4,
∴CD=![]() BC=2,CE=
BC=2,CE=![]() CD=1,DE=CDcos30°=
CD=1,DE=CDcos30°=![]() ,
,
∴S阴=S四边形ODEC﹣S扇形ODC=![]() (1+2)×
(1+2)×![]() ﹣
﹣![]() =
=![]() ﹣
﹣![]() .
.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目