题目内容
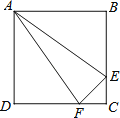
【题目】已知，如图，点B、F、C、E在同一直线上，AC、DF相交于点G，AB⊥BE，垂足为B，DE⊥BE，垂足为E，且AC=DF，BF=EC．求证：
（1）△ABC≌△DEF；
（2）FG=CG．
【答案】见解析
【解析】
试题分析：（1）首先利用等式的性质可得BC=EF，再有条件AC=DF可利用HL定理证明Rt△ABC≌Rt△DEF；
（2）根据全等三角形的性质得到∠ACB=∠DFE，根据等腰三角形的性质即可得到结论
证明：（1）∵BF=CE
∴BF+FC=CF+FC，
∴BC=EF，
∵AB⊥BE，DE⊥BE，
∴∠B=∠E=90°，
在Rt△ABC和Rt△DEF中，
，
∴Rt△ABC≌Rt△DEF（HL）；
（2）∵Rt△ABC≌Rt△DEF，
∴∠ACB=∠DFE，
∴FG=CG．
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
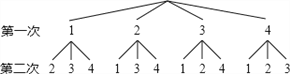
点睛新教材全能解读系列答案【题目】在不透明的袋子中有四张标着数字1，2，3，4的卡片，小明、小华两人按照各自的规则玩抽卡片游戏．小明画出树状图如图所示：
小华列出表格如下：
1 | 2 | 3 | 4 | |
1 | （1，1） | （2，1） | （3，1） | （4，1） |
2 | （1，2） | （2，2） | ① | （4，2） |
3 | （1，3） | （2，3） | （3，3） | （4，3） |
4 | （1，4） | （2，4） | （3，4） | （4，4） |
（1）根据树形图分析，小明的游戏规则是，随机抽出一张卡片后 （填“放回”或“不放回”），再随机抽出一张卡片；根据表格分析，小华的游戏规则是，随机抽出一张卡片后 （填“放回”或“不放回”），再随机抽出一张卡片。
（2）根据小华的游戏规则，表格中①表示的有序数对为 。
（3）规定两次抽到的数字之和为奇数的获胜，谁获胜的可能性大？为什么？
【题目】甲、乙两人在5次打靶测试中命中的环数如下：
甲：8，8，7，8，9
乙：5，9，7，10，9
（1）填写下表：
平均数 | 众数 | 中位数 | 方差 | |
甲 | 8 | 8 | 0.4 | |
乙 | 9 | 3.2 |
（2）教练根据这5次成绩，选择甲参加射击比赛，教练的理由是什么？
（3）如果乙再射击1次，命中8环，那么乙的射击成绩的方差 ．（填“变大”、“变小”或“不变”）．
