题目内容
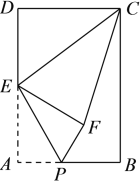
【题目】已知：在△ABC中，∠A=90°，AB=6，AC=8，点P在边AC上，且⊙P与AB，BC都相切．
（1）求⊙P半径；
（2）求sin∠PBC．
【答案】（1）⊙P半径为3；（2）sin∠PBC=
．
【解析】
（1）过P作PE⊥BC，由⊙P与AB，BC都相切，可得BA=BE=6，PA=PE，然后根据S△ABC的面积=S△ABP+S△BCP计算即可；
（2）在Rt△BPE中，先根据勾股定理求出BP的长，然后利用三角函数解答即可．
（1）如图所示：
过P作PE⊥BC，
∵⊙P与AB，BC都相切，
∴BA=BE=6，PA=PE，
∵在△ABC中，∠A=90°，AB=6，AC=8，
∴△ABC的面积=
，
即
，
解得：PA=3，
即⊙P半径=3；
（2）在Rt△BPE中，BP=
，
∴sin∠PBC=
．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案【题目】阅读对学生的成长有着深远的影响，某中学为了解学生每周课余阅读的时间，在本校随机抽取了若干名学生进行调查，并依据调查结果绘制了以下不完整的统计图表．
组别 | 时间（小时） | 频数（人数） | 频率 |
A | 0≤t≤0.5 | 6 | 0.15 |
B | 0.5≤t≤1 | a | 0.3 |
C | 1≤t≤1.5 | 10 | 0.25 |
D | 1.5≤t≤2 | 8 | b |
E | 2≤t≤2.5 | 4 | 0.1 |
合计 | 1 |
请根据图表中的信息，解答下列问题：
（1）表中的a= ，b= ，中位数落在 组，将频数分布直方图补全；
（2）估计该校2000名学生中，每周课余阅读时间不足0.5小时的学生大约有多少名？
（3）E组的4人中，有1名男生和3名女生，该校计划在E组学生中随机选出两人向全校同学作读书心得报告，请用画树状图或列表法求抽取的两名学生刚好是1名男生和1名女生的概率．
【题目】抛物线
上部分点的横坐标
，纵坐标
的对应值如下表：
| … |
|
|
|
|
| … |
| … |
|
|
|
|
| … |
根据上表填空：
①抛物线与轴的交点坐标是________和________；
②抛物线经过点
,________
；
③在对称轴右侧，随增大而________；
试确定抛物线的解析式．
