题目内容
【题目】已知△ABC中,∠CAB=90°,AC=AB=3,△CDE中,∠CDE=90°,CD=DE=5,连接BE,取BE中点F,连接AF、DF.

(1)如图1,若C、B、E三点共线,H为BC中点.
①直接指出AF与DF的关系 ;
②直接指出FH的长度 ;
(2)将图(1)中的△CDE绕C点逆时针旋转a(如图2,0°<α<180°),试确定AF与DF的关系,并说明理由;
(3)在(2)中,若AF=![]() ,请直接指出点F所经历的路径长.
,请直接指出点F所经历的路径长.
【答案】(1)①AF=DF,且AF⊥DF;②![]() ;(2)结论:AF=DF,且AF⊥DF(3)当旋转30°或150°时,AF=
;(2)结论:AF=DF,且AF⊥DF(3)当旋转30°或150°时,AF=![]() ,点F经历的路径长为
,点F经历的路径长为![]() 或
或![]()
【解析】
(1)①AF=DF,且AF⊥DF,如图1,过F作MN∥CD,交DE于M,交CA的延长线于N,根据已知条件易证四边形FMCN为矩形,再证△FNA≌△FMD,即可得DF=AF,∠AFN=∠FDM,再由∠FDM+∠MFD=90°,可得∠MFD+∠AFN=90°,即∠DFA=90°,所以DF⊥AF; ②因H是BC的中点,可得BH=![]() BC,由FH=BF+BH即可解答;(2) AF=DF,且AF⊥DF,延长AF至S使FS=AF,连接DS、SE,延长SE交AC于T,先证△ABF≌△SEF,再证△SED≌△ACD,即可证得结论;(3) 分旋转30°或150°两种情况求点F所经历的路径长.
BC,由FH=BF+BH即可解答;(2) AF=DF,且AF⊥DF,延长AF至S使FS=AF,连接DS、SE,延长SE交AC于T,先证△ABF≌△SEF,再证△SED≌△ACD,即可证得结论;(3) 分旋转30°或150°两种情况求点F所经历的路径长.
(1)①AF=DF,且AF⊥DF,
理由是:如图1,过F作MN∥CD,交DE于M,交CA的延长线于N,

∵△ABC是等腰直角三角形,且AC=3,
∴BC=3![]() ,
,
同理EC=5![]() ,
,
∵C、B、E三点共线,
∴EB=5![]() ﹣3
﹣3![]() =2
=2![]() ,
,
∵F是BE的中点,
∴EF=![]() BE=
BE=![]() ,
,
∵∠E=45°,
∴EM=FM=1,
∴DM=5﹣1=4,
∵∠ECD+∠ACB=45°+45°=90°
∴∠EDC=∠ACD=∠MNC=90°,
∴四边形MDCN是矩形,
∴CN=DM=4,MN=DC=5,
∴FN=DM=4,FM=AN=1,
∵∠DMF=∠FNA=90°,
∴△FNA≌△DMF,
∴DF=AF,∠AFN=∠FDM,
∵∠FDM+∠MFD=90°,
∴∠MFD+∠AFN=90°,
∴∠DFA=90°,
∴DF⊥AF;
②∵H是BC的中点,
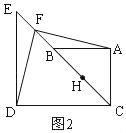
∴BH=![]() BC=
BC=![]() ,
,
∴FH=BF+BH=![]() +
+![]() =
=![]() ;
;
故答案为:①AF=DF,且AF⊥DF;②![]() ;
;
(2)结论:AF=DF,且AF⊥DF,
理由如下:
延长AF至S使FS=AF,连接DS、SE,延长SE交AC于T,
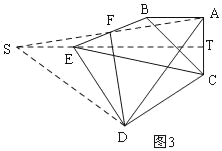
∵∠AFB=∠EFS,BF=EF,
∴△ABF≌△SEF,
∴AB=SE=AC,∠FAB=∠FSE,
∴∠STC=∠BAC=90°,
∴∠EDC+∠STC=180°,
∴∠TED+∠TCD=180°,
∵∠TED+∠SED=180°,
∴∠SED=∠ACD,
∵ED=CD,
∴△SED≌△ACD,
∴AD=SD,∠ADC=∠SDE,
∴∠ADS=90°,
∴AF=DF,且AF⊥DF;
(3)∵F是BE的中点,H是BC的中点,
∴FH是△BEC的中位线,
∴FH=![]() EC=
EC=![]() ,
,
∵在旋转过程中,CE是定值,则FH也是定值,
∴点F的运动路径是以H为中点,以FH为半径的圆,
如图4,过D作DM⊥AC,交AC的延长线于M,
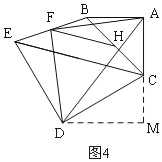
由(2)知:△AFD是等腰直角三角形,
∵AF=![]() ,
,
∴AD=![]() ×
×![]() =7,
=7,
设CM=x,DM=y,
则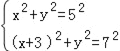 ,
,
解得:x=![]() ,
,
∴CM=![]() ,
,
∵CD=5,
∴∠CDM=30°,
∴∠DCM=60°,
∵∠ACB+∠DCE+∠BCE+∠DCM=180°,
∴∠BCE=30°,即α=30°,
此时,点F所经历的路径长=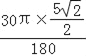 =
=![]() .
.
如图5,过D作DM⊥AC,交AC的延长线于M,
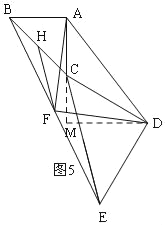
同理得:∠DCM=60°,
∵∠ECD=45°,
∴∠ECM=60°﹣45°=15°,
∴α=∠BCE=180°﹣45°+15°=150°,
此时,点F所经历的路径长=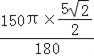 =
=![]() .
.
综上所述,当旋转30°或150°时,AF=![]() ,点F经历的路径长为
,点F经历的路径长为![]() 或
或![]() .
.

【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() ,纵坐标
,纵坐标![]() 的对应值如下表:
的对应值如下表:
| … |
|
|
|
|
| … |
| … |
|
|
|
|
| … |
![]() 根据上表填空:
根据上表填空:
①抛物线与![]() 轴的交点坐标是________和________;
轴的交点坐标是________和________;
②抛物线经过点![]() ,________
,________![]() ;
;
③在对称轴右侧,![]() 随
随![]() 增大而________;
增大而________;
![]() 试确定抛物线
试确定抛物线![]() 的解析式.
的解析式.





