题目内容
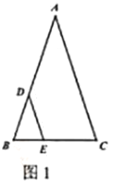
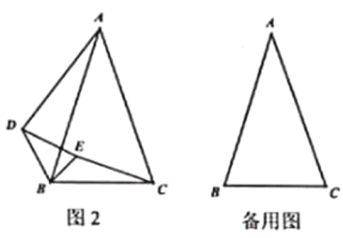
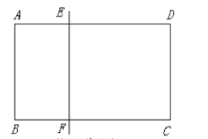
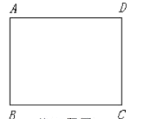
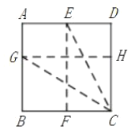
【题目】如图,![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上一点.以
边上一点.以![]() 为圆心
为圆心![]() 长为半径的⊙O与
长为半径的⊙O与![]() 边相切于
边相切于![]() 点,与边
点,与边![]() 相交于点
相交于点![]() ,连接
,连接![]() 交⊙O于点
交⊙O于点![]() ,连接
,连接![]() .
.
(1)求证:![]() .
.
(2)若⊙O的半径为![]() .
.
①当![]() 的长为 时,四边形
的长为 时,四边形![]() 为菱形;
为菱形;
②若![]() .则
.则![]() 的长为 .
的长为 .
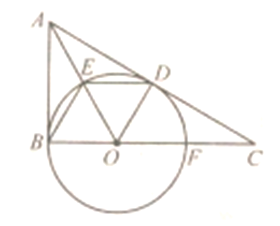
【答案】(1)证明见解析;(2)①![]() ;②
;②![]()
【解析】
(1)利用全等三角形的判定证明![]() 即可证明结论;
即可证明结论;
(2)①运用菱形的性质可得![]() 均为等边三角形,即可得出∠BOD的度数,即可求得
均为等边三角形,即可得出∠BOD的度数,即可求得![]() 的长;
的长;
②利用勾股定理求出CD的长度,再利用勾股定理列出方程,求解即可得出答案.
(1)∵⊙O与![]() 边相切于
边相切于![]() 点,
点,
∴∠ADO=90°,
∴∠ADO=∠ABO=90°,
又∵OB=OD,OA=OA,
∴![]() ,
,
∴∠AOB=∠AOD,
∴![]() ,
,
∴BE=ED.
(2)①∵四边形![]() 为菱形,
为菱形,
∴BE=BO=ED=OD,
∵OB=OE,
∴OB=OE=BE,OE=ED=OD,
∴![]() 均为等边三角形,
均为等边三角形,
∴∠BOE=∠EOD=60°,
∴∠BOD=120°,
∴![]() 的长为
的长为![]() ,
,
∴![]() 的长为
的长为![]() 时,四边形
时,四边形![]() 为菱形.
为菱形.
故答案为:![]() .
.
②设AD=x,
∵![]() ,
,
∴AB=AD=x,
在![]() 中,OC=3+2=5,OD=3,
中,OC=3+2=5,OD=3,
∴CD=![]() ,
,
∴AC=x+4,
在Rt△ABC中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
故答案为:6.

练习册系列答案
相关题目
【题目】红旗连锁超市准备购进甲、乙两种绿色袋装食品.甲、乙两种绿色袋装食品的进价和售价如表.已知:用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同.
甲 | 乙 | |
进价(元/袋) |
|
|
售价(元/袋) | 20 | 13 |
(1)求![]() 的值;
的值;
(2)要使购进的甲、乙两种绿色袋装食品共800袋的总利润(利润=售价-进价)不少于4800元,且不超过4900元,问该超市有几种进货方案?
(3)在(2)的条件下,该超市如果对甲种袋裝食品每袋优惠![]() 元出售,乙种袋装食品价格不变.那么该超市要获得最大利润应如何进货?
元出售,乙种袋装食品价格不变.那么该超市要获得最大利润应如何进货?