题目内容
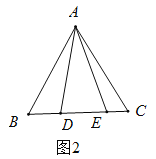
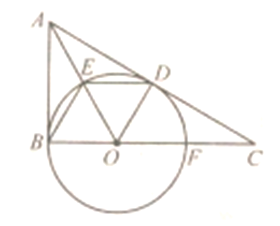
【题目】已知OA是⊙O的半径,OA=1,点P是OA上一动点,过P作弦BC⊥OA,连接AB、AC.

(1)如图1,若P为OA中点,则AC=______,∠ACB=_______°;
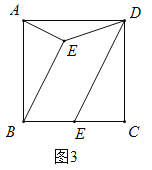
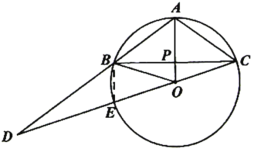
(2)如图2,若移动点P,使AB、CO的延长线交于点D.记△AOC的面积为S1,△BOD的面积为S2.△AOD的面积为S3,且满足![]() ,求
,求![]() 的值.
的值.
【答案】(1)1,30;(2)![]() .
.
【解析】
(1)证得△AOC为等边三角形,得出AC=1,∠ACO=60°,可求出答案;
(2)若DC与圆O相交于点E,连接BE,证明△ABO≌△ACO(SSS),得出S△ABO=S△ACO=S1,由题意得出(![]() )2+
)2+![]() 1=0,解得:
1=0,解得:![]() =
=![]() ,求出
,求出![]() ,证明△AOD∽△BED,得出
,证明△AOD∽△BED,得出![]() =
=![]() ,得出OP=
,得出OP=![]() BE,则可求出答案.
BE,则可求出答案.
解:(1)∵BC⊥OA,OB=OC,
∴BP=CP,
∵P是OA的中点,
∴OP=AP,
∴OA垂直平分BC,且BC垂直平分OA,
∴四边形ABOC是菱形,
∴AC=OC=OA=1,BC平分∠ACO,
∴△AOC是等边三角形,
∴∠ACO=60°,
∴∠ACB=![]() ∠ACO=30°,
∠ACO=30°,
故答案为:1,30;
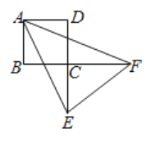
(2)连接![]() ,
,
∵![]()
∴![]() ,
,
∴![]() ,
,
∵![]() ,AO=AO,
,AO=AO,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴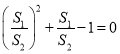 ,
,
解得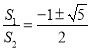 ,
,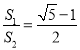 ,
,
∴![]() ,即
,即![]() ,
,
∵![]() 为直径,
为直径,
∴![]() ,
,
∴![]() ,
,
∴![]()
∴![]() ,
,
∵![]()
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
∴![]() .
.

【题目】某超市计划购进一批A、B两种规格的端午节礼盘进行销售,进价和售价如下表所示:
端午节礼盘规格 | A | B |
进价(元/盘) | 80 | 100 |
售价(元/盘) | 120 | 160 |
若购进两种规格的端午节礼盒共300盒,且投入资金不超过26800元.
(1)该超市应购进A规格端午节礼盒至少多少盒?
(2)若超市购进A规格端午节礼盒的进价每盒降低a元,并保持这两个规格的端午节礼盒的售价不变,且最多购进240盒A规格端午节礼盒.如果这批端午节礼盒售出后,超市刚好获利18480元,求a的取值范围.
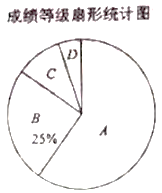
【题目】钟南山院士谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,但也不必恐慌,尽量少去人员密集的场所,出门戴口罩,在室内注意通风,勤洗手,多运动,少熬夜.”某学校为了了解学生对新型冠状病毒肺炎防护知识的掌握情况,随机抽取若干名同学利用网络进行了“新冠状病毒肺炎防疫知识”问卷测试.根据测试成绩分布情况,他们将全部测试成绩分成![]() 、
、![]() 、
、![]() 、
、![]() 四组,绘制了如下统计图表:
四组,绘制了如下统计图表:
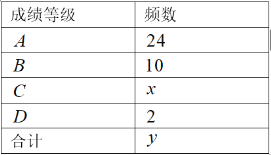
“新冠状病毒肺炎防疫知识”问卷测试成绩统计表
组别 | 分数/分 | 频数 | 各组总分/分 |
|
| 38 | 2581 |
|
|
| 5543 |
|
| 60 | 5100 |
|
| 30 | 2796 |
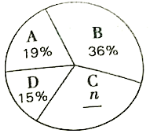
依据以上统计信息,解答下列问题:
(1)求得![]() ,
,![]() ;
;
(2)这次测试成绩的中位数落在 组;
(3)求本次全部测试成绩的平均数.