题目内容
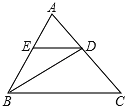
【题目】已知:如图(1)所示,在△ABC中,BD平分∠ABC , CD平分∠ACB,过D点作EF∥BC,与AB交于点E,与AC交于点F
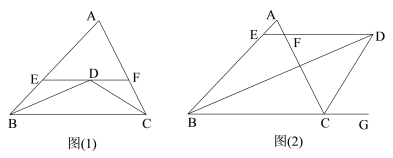
(1)若BE=3,CF=2,求EF的长;
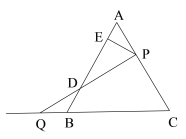
(2)如图(2)所示,若∠ABC的平分线BD与△ABC的外角∠ACG的平分线CD相交于点D,其它条件不变,请写出EF,BE,CF之间的数量关系,并说明理由.
【答案】(1)EF=5;(2)EF=BE-CF,见解析
【解析】
(1)根据角平分线的性质和平行线的性质得到DE=BE,DF=CF,由此得到EF的长度;
(2)根据平行线的性质及角平分线的性质证得BE=DE,CF=DF,即可得到BE=EF+CF.
(1)∵BD平分∠ABC,
∴∠EBD=∠DBC,
∵EF∥BC,
∴∠EDB=∠DBC,
∴∠EBD=∠EDB,
∴DE=BE=3,
同理:DF=CF=2,
∴EF=DE+DF=5;
(2)EF=BE-CF理由如下:
∵ED∥BC,
∴∠EDB=∠DBC,∠EDC=∠DCG,
∵BD平分∠ABC , CD平分∠ACG,
∴∠EBD=∠DBC,∠ACD=∠DCG,
∴∠EDB=∠EBD,∠ACD=∠EDC,
∴BE=DE,CF=DF,
又∵DE=EF+DF,
∴BE=EF+CF,
∴EF=BE-CF.

练习册系列答案
相关题目