题目内容
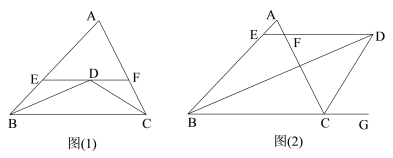
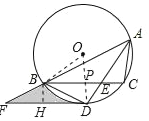
【题目】如图,△ABC内接于⊙O,∠BAC的平分线交⊙O于点D,交BC于点E(BE>EC),且BD=2![]() .过点D作DF∥BC,交AB的延长线于点F.
.过点D作DF∥BC,交AB的延长线于点F.
(1)求证:DF为⊙O的切线;
(2)若∠BAC=60°,DE=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.

【答案】(1)详见解析;(2)9![]() ﹣2π.
﹣2π.
【解析】
(1)连结OD,根据垂径定理得到OD⊥BC,根据平行线的性质得到OD⊥DF,根据切线的判定定理证明;
(2)连结OB,连结OD交BC于P,作BH⊥DF于H,证明△OBD为等边三角形,得到∠ODB=60°,OB=BD=2![]() ,根据勾股定理求出PE,证明△ABE∽△AFD,根据相似三角形的性质求出AE,根据阴影部分的面积=△BDF的面积-弓形BD的面积计算.
,根据勾股定理求出PE,证明△ABE∽△AFD,根据相似三角形的性质求出AE,根据阴影部分的面积=△BDF的面积-弓形BD的面积计算.
证明:(1)连结OD,
∵AD平分∠BAC交⊙O于D,
∴∠BAD=∠CAD,
∴![]() ,
,
∴OD⊥BC,
∵BC∥DF,
∴OD⊥DF,
∴DF为⊙O的切线;
(2)连结OB,连结OD交BC于P,作BH⊥DF于H,
∵∠BAC=60°,AD平分∠BAC,
∴∠BAD=30°,
∴∠BOD=2∠BAD=60°,
∴△OBD为等边三角形,
∴∠ODB=60°,OB=BD=2![]() ,
,
∴∠BDF=30°,
∵BC∥DF,
∴∠DBP=30°,
在Rt△DBP中,PD=![]() BD=
BD=![]() ,PB=
,PB=![]() PD=3,
PD=3,
在Rt△DEP中,∵PD=![]() ,DE=
,DE=![]() ,
,
∴PE=![]() =2,
=2,
∵OP⊥BC,
∴BP=CP=3,
∴CE=3﹣2=1,
∵∠DBE=∠CAE,∠BED=∠AEC,
∴△BDE∽△ACE,
∴AE:BE=CE:DE,即AE:5=1:![]() ,
,
∴AE=![]()
∵BE∥DF,
∴△ABE∽△AFD,
∴![]() ,即
,即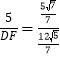 ,
,
解得DF=12,
在Rt△BDH中,BH=![]() BD=
BD=![]() ,
,
∴阴影部分的面积=△BDF的面积﹣弓形BD的面积=△BDF的面积﹣(扇形BOD的面积﹣△BOD的面积)=![]() =9
=9![]() ﹣2π.
﹣2π.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】在不透明的袋子中有四张标有数字1,2,3,4的卡片,小明、小华两人按照各自的规则玩抽卡片游戏。
小明画出树形图如下:

小华列出表格如下:
第一次 第二次 | 1 | 2 | 3 | 4 |
1 | (1,1) | (2,1) | (3,1) | (4,1) |
2 | (1,2) | (2,2) | ① | (4,2) |
3 | (1,3) | (2,3) | (3,3) | (4,3) |
4 | (1,4) | (2,4) | (3,4) | (4,4) |
回答下列问题:
(1)根据小明画出的树形图分析,他的游戏规则是:随机抽出一张卡片后 (填“放回”或“不放回”),再随机抽出一张卡片;
(2)根据小华的游戏规则,表格中①表示的有序数对为 ;
(3)规定两次抽到的数字之和为奇数的获胜,你认为淮获胜的可能性大?为什么?