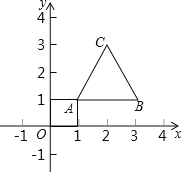Question

【题目】如图，在△ABC中，∠ACB=2∠A，过点C的直线能将△ABC分成两个等腰三角形，则∠A的度数为____．

Answer 1

【答案】45°或36°或()°．

【解析】

根据等腰三角形的性质和三角形的内角和即可得到结论．

∵过点C的直线能将△ABC分成两个等腰三角形，

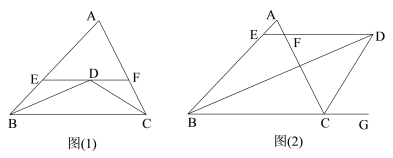
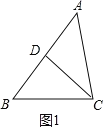
①如图1．

∵∠ACB=2∠A，∴AD=DC=BD，

∴∠ACB=90°，

∴∠A=45°；

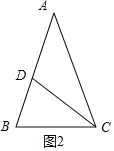
②如图2，AD=DC=BC，

∴∠A=∠ACD，∠BDC=∠B，

∴∠BDC=2∠A，

∴∠A=36°，

③AD=DC，BD=BC，

∴∠BDC=∠BCD，∠A=∠ACD，

∴∠BCD=∠BDC=2∠A，

∴∠BCD=2∠A．

∵∠ACB=2∠A，故这种情况不存在．

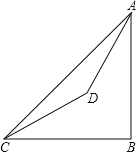
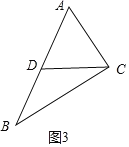
④如图3，AD=AC，BD=CD，

∴∠ADC=∠ACD，∠B=∠BCD，

设∠B=∠BCD=α，

∴∠ADC=∠ACD=2α，

∴∠ACB=3α，

∴∠A=α．

∵∠A+∠B+∠ACB=180°，

∴ α+α+3α=180°，

∴α= ，

∴∠A=，

综上所述：∠A的度数为45°或36°或()°．

故答案为：45°或36°或()°．