题目内容
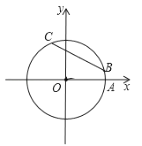
【题目】如图，在平面直角坐标系xOy中，以原点O为圆心的圆过点A（
，0），直线y=kx－2k＋3与⊙O交于B、C两点，则弦BC的长的最小值为_______．
【答案】8
【解析】
易知直线y=kx-2k+3过定点D(2,3),运用勾股定理可求出OD,由条件可求出半径OB,由于过圆内定点D的所有弦中,与OD垂直的弦最短,因此只需运用垂径定理及勾股定理就可解决问题.
对于直线y=kx-2k+3=k(x-2)+3,当x=2时,y=3,故直线y=kx-2k+3恒经过点(2,3),记为点D.过点D作DH⊥x轴于点H,如下图所示
∴OH=2,DH=3,OD=
=
∵点A(
,0),
∴OA=,
∴OB=OA=
由于过圆内定点D的所有弦中,与OD垂直的弦最短
因此运用垂径定理及勾股定理可得:
BC的最小值为2BD=2
=2x
=2×4=8
练习册系列答案
相关题目
