题目内容
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b>0;②abc<0;③b2﹣4ac>0;④a+b+c<0;⑤4a﹣2b+c<0,其中正确的个数是( ) 
A.2
B.3
C.4
D.5
【答案】B
【解析】解:①∵抛物线开口向下, ∴a<0,
∵对称轴x=﹣ ![]() >1,
>1,
∴2a+b>0,故①正确;
②∵a<0,﹣ ![]() >0,
>0,
∴b>0,
∵抛物线与y轴的交点在x轴的下方,
∴c<0,
∴abc>0,故②错误;
③∵抛物线与x轴有两个交点,
∴△=b2﹣4ac>0,故③正确;
④∵x=1时,y>0,
∴a+b+c>0,故④错误;
⑤∵x=﹣2时,y<0,
∴4a﹣2b+c<0,故⑤正确.
故选:B.
【考点精析】解答此题的关键在于理解二次函数图象以及系数a、b、c的关系的相关知识,掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).

练习册系列答案
相关题目
【题目】按下列程序计算,把答案填写在表格内,然后观察有什么规律,想一想:为什么会有这个规律?
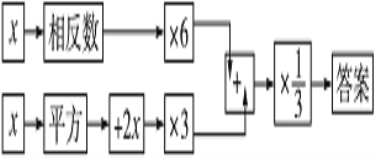
(1)填写表内空格:
输入 | -3 | -2 | -1 | 0 | … |
输出答案 | 9 |
|
|
| … |
(2)发现的规律是:输入数据x,则输出的答案是__________;
(3)为什么会有这个规律?请你说明理由.